Cho hình vẽ
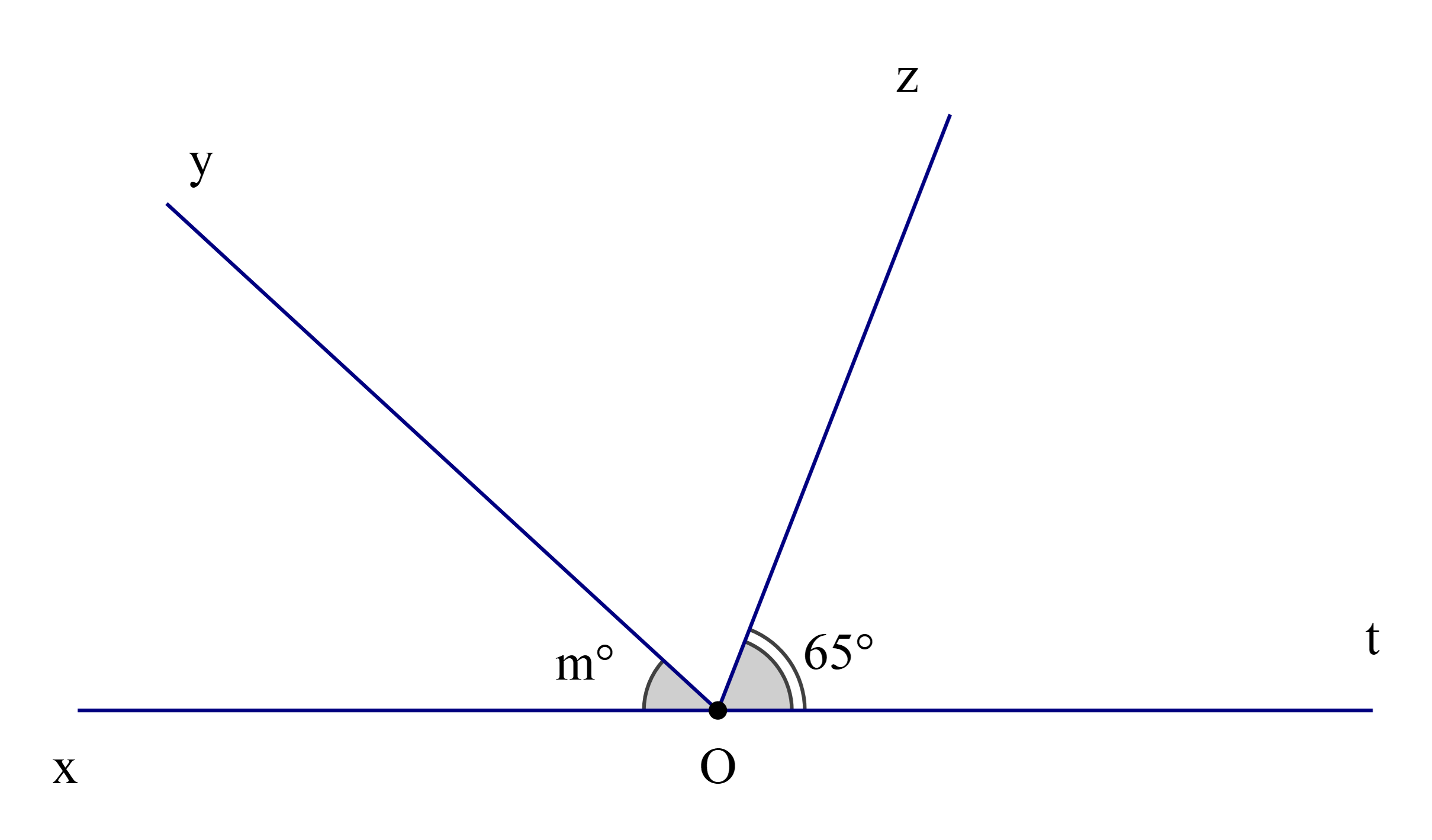
Giá trị của m để tia Oz là tia phân giác của \(\widehat {{\rm{yOt}}}\) là:
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: A
Để tia Oz là tia phân giác của \(\widehat {{\rm{yOt}}}\) thì \(\widehat {{\rm{yOz}}} = \widehat {{\rm{zOt}}}\) (1)
Mà \(\widehat {{\rm{yOz}}} + \widehat {{\rm{zOt}}} = \widehat {{\rm{yOt}}}\) (hai góc kề nhau) (2)
Từ (1) và (2) suy ra \(\widehat {{\rm{yOz}}} = \widehat {{\rm{zOt}}} = \frac{{\widehat {{\rm{yOt}}}}}{2}\)
Suy ra \(\widehat {{\rm{yOt}}} = 2\widehat {{\rm{zOt}}} = 2.65^\circ = 130^\circ \)
Ta lại có \(\widehat {xOy} + \widehat {{\rm{yOt}}} = 180^\circ \) (hai góc kề bù)
Suy ra \(\widehat {{\rm{xOy}}} = 180^\circ - \widehat {yOt} = 180^\circ - 130^\circ = 50^\circ \)
Do đó m = 50
Vậy ta chọn phương án A.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho hình vẽ:

Biết rằng EF // BC. Số đo của \(\widehat {BEF}\) là:
Cho hình vẽ. Biết rằng x // y; đường thẳng z cắt hai đường thẳng x, y lần lượt tại A, B sao cho \({\widehat {\rm{A}}_1} = 60^\circ \).
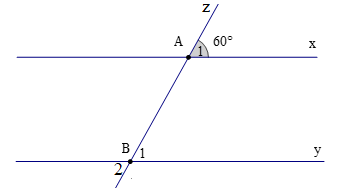
Số đó của \({\widehat {\rm{B}}_2}\) là:
Cho hình vẽ, biết rằng OB là tia phân giác của \(\widehat {{\rm{AOC}}}\).
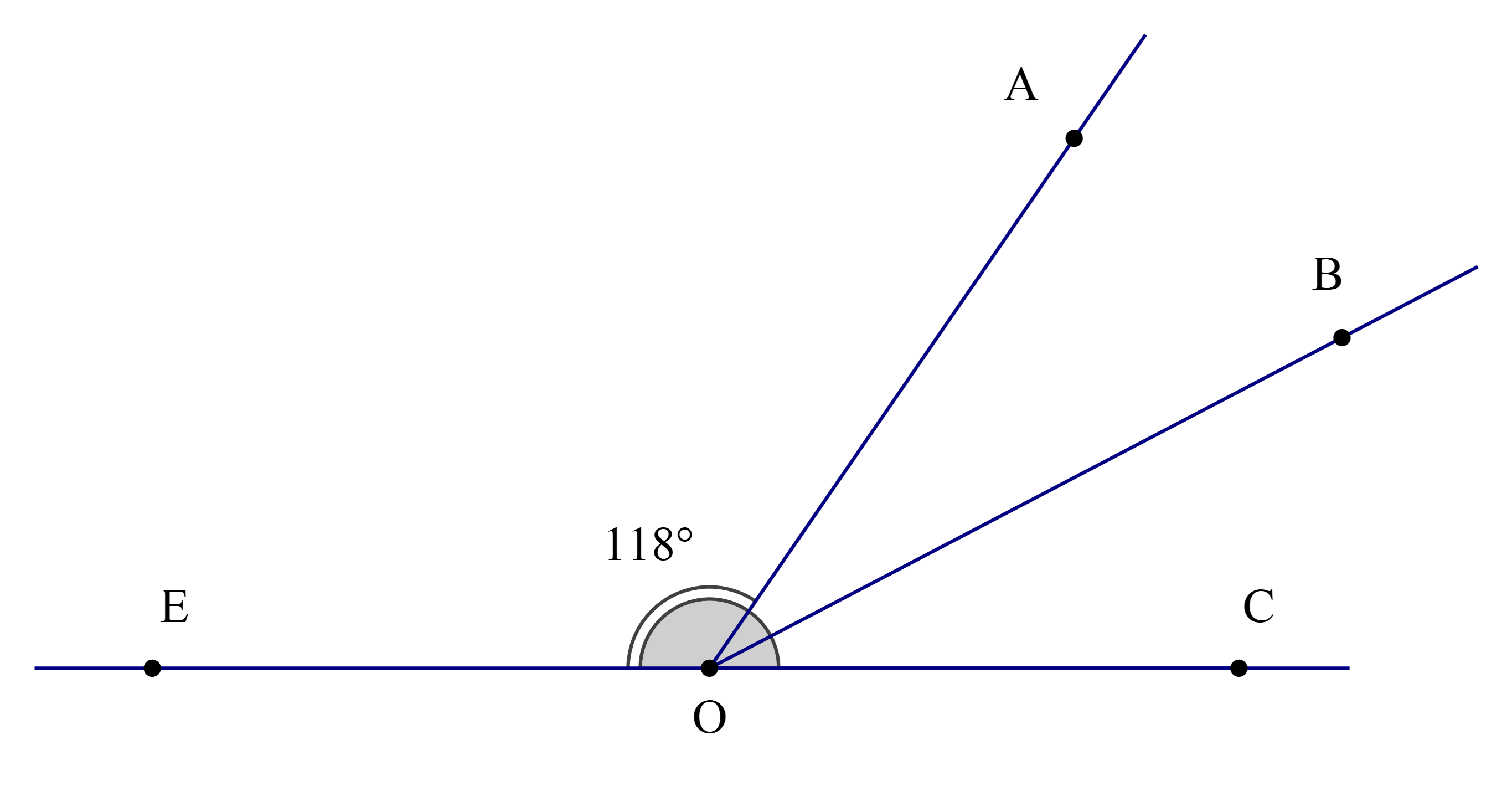
Số đo của \(\widehat {{\rm{BOC}}}\)là
Một định lí được minh họa bởi hình vẽ:
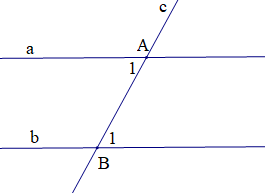
Định lí có giả thiết và kết luận như sau:
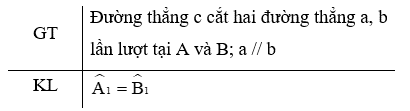
Định lí được phát biểu thành lời là:
Cho hình vẽ, biết rằng \(\widehat {{\rm{xOy}}} = 110^\circ \) và Oz là phân giác của \(\widehat {{\rm{yOt}}}\).
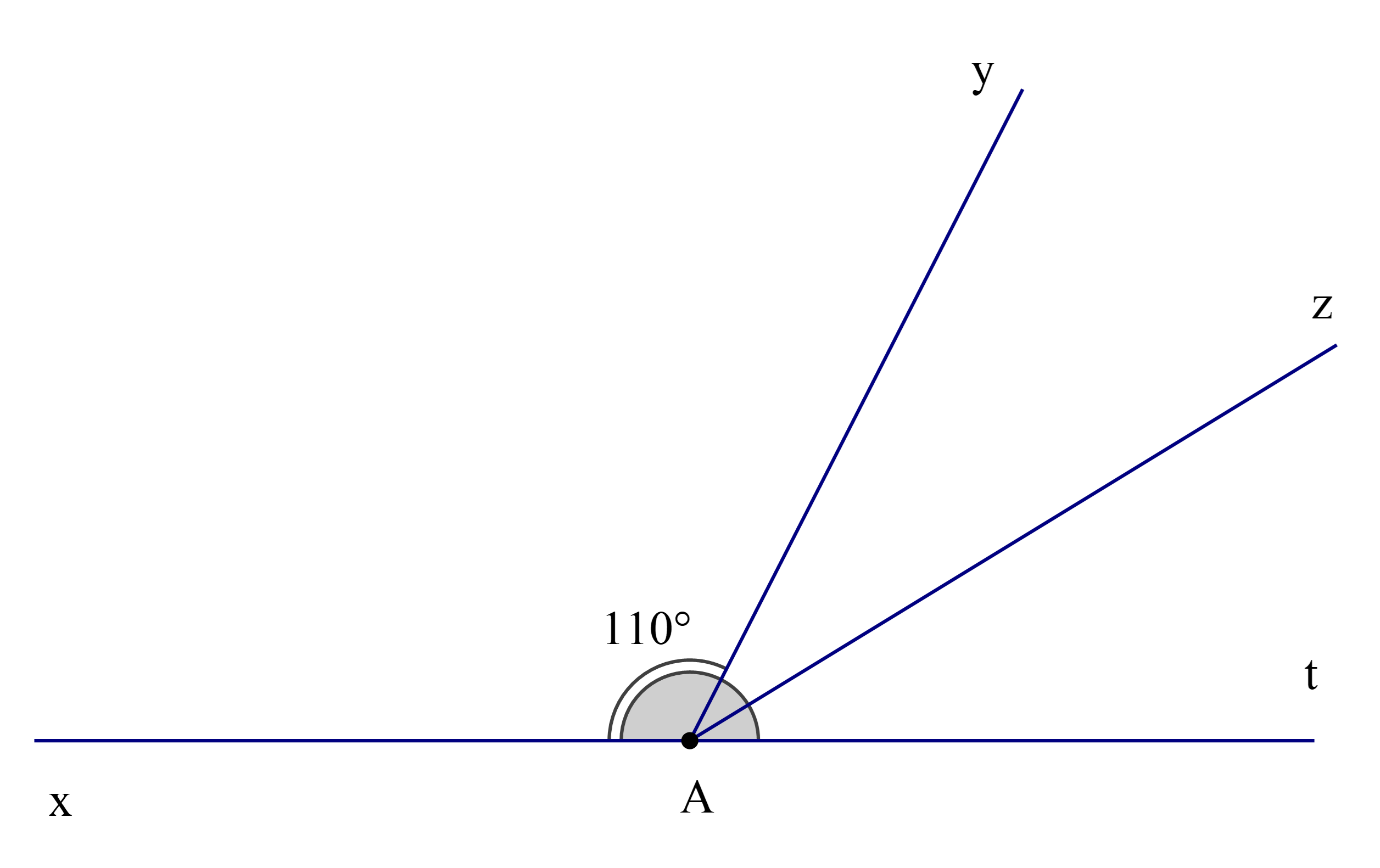
Số đo của \(\widehat {{\rm{xOz}}}\)là