Trắc nghiệm Toán 7 Bài tập cuối tập chương 4 có đáp án (Thông hiểu)
-
614 lượt thi
-
8 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Cho hình vẽ, biết rằng OB là tia phân giác của \(\widehat {{\rm{AOC}}}\).
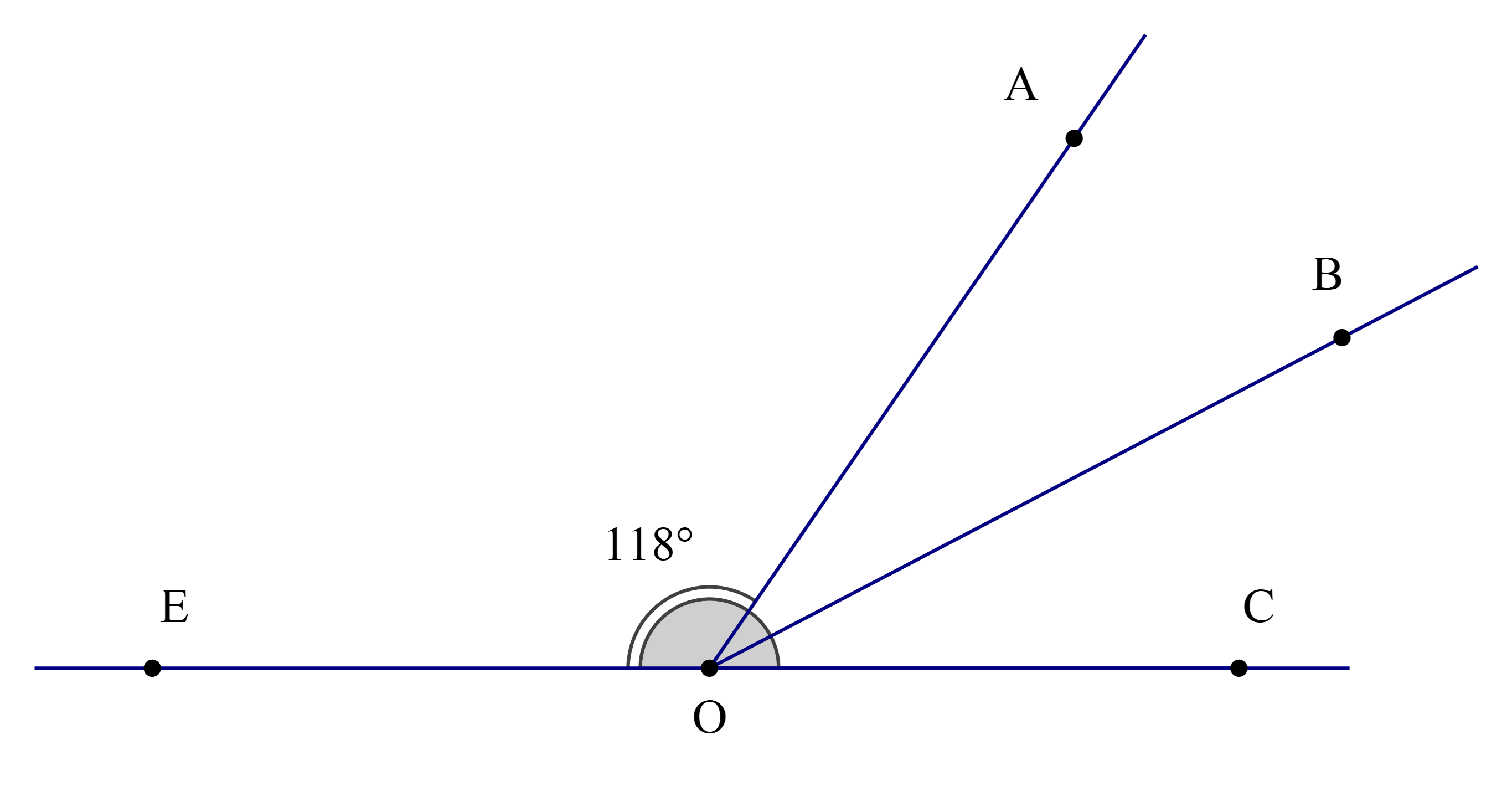
Số đo của \(\widehat {{\rm{BOC}}}\)là
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
Ta có \(\widehat {{\rm{EOA}}}\) và \(\widehat {{\rm{AOC}}}\) là hai góc kề bù nên \(\widehat {{\rm{EOA}}} + \widehat {{\rm{AOC}}} = 180^\circ \)
Hay \(118^\circ + \widehat {{\rm{AOC}}} = 180^\circ \)
Suy ra \(\widehat {{\rm{AOC}}} = 180^\circ - 118^\circ = 62^\circ \)
Theo bài ta có OB là tia phân giác của \(\widehat {{\rm{AOC}}}\)
Do đó \(\widehat {{\rm{AOB}}} = \widehat {{\rm{BOC}}}\) (tính chất tia phân giác của một góc) (1)
Mà \(\widehat {{\rm{AOB}}} + \widehat {{\rm{BOC}}} = \widehat {{\rm{AOC}}}\) (hai góc kề nhau) (2)
Từ (1) và (2) suy ra \(\widehat {{\rm{AOB}}} = \widehat {{\rm{BOC}}} = \frac{1}{2}\widehat {{\rm{AOC}}}\)
Hay \(\widehat {{\rm{BOC}}} = \frac{1}{2}.62^\circ = 31^\circ \)
Vậy ta chọn phương án B.
Câu 2:
Cho hình vẽ, biết rằng \(\widehat {{\rm{xOy}}} = 110^\circ \) và Oz là phân giác của \(\widehat {{\rm{yOt}}}\).
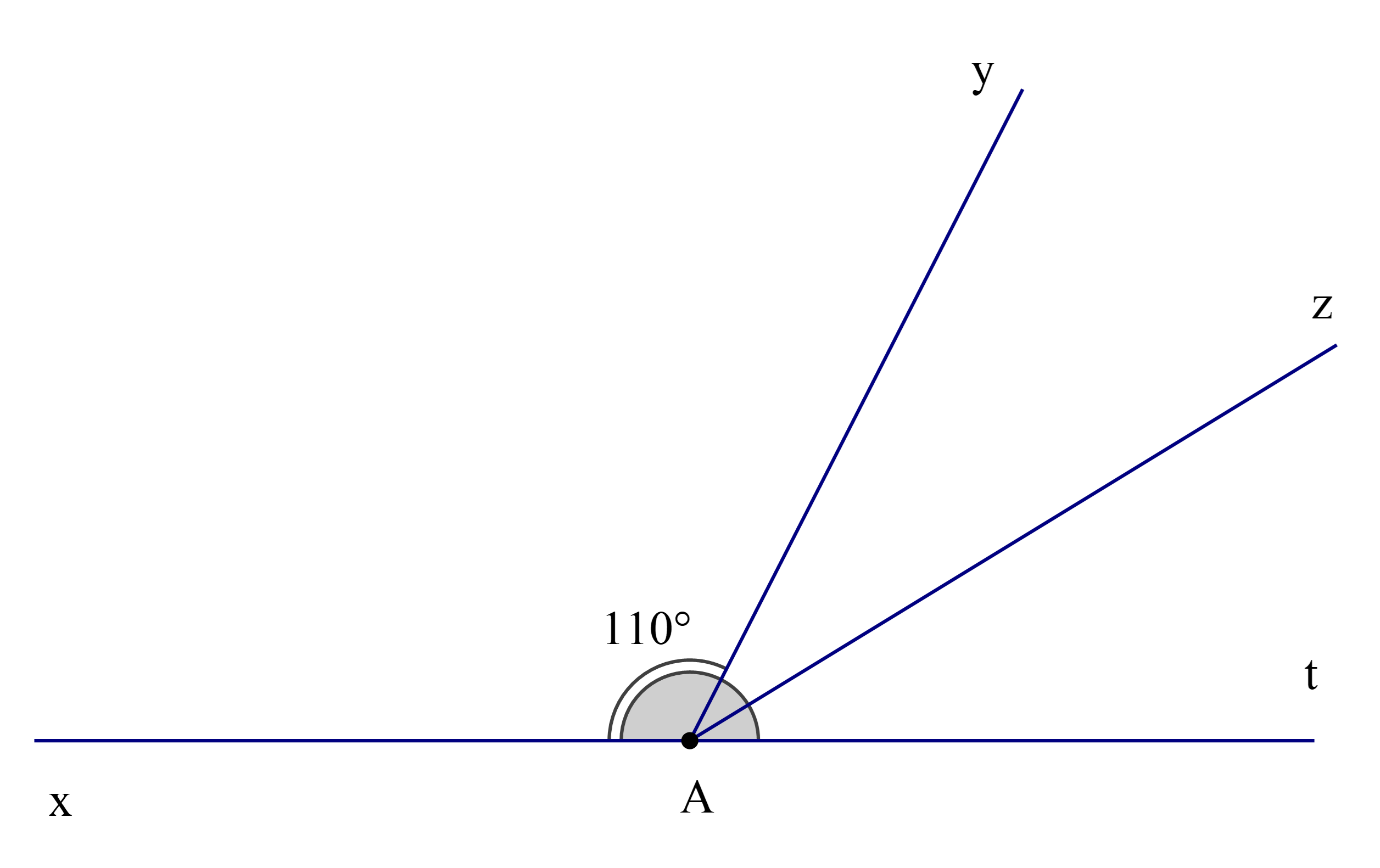
Số đo của \(\widehat {{\rm{xOz}}}\)là
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
Ta có \(\widehat {{\rm{xOy}}} + \widehat {{\rm{yOt}}} = 180^\circ \) (hai góc kề bù)
Hay \(110^\circ + \widehat {{\rm{yOt}}} = 180^\circ \)
Suy ra \(\widehat {{\rm{yOt}}} = 180^\circ - 110^\circ = 70^\circ \)
Theo bài ta có Oz là phân giác của \(\widehat {{\rm{yOt}}}\)
Suy ra \(\widehat {{\rm{yOz}}} = \widehat {{\rm{zOt}}}\) (tính chất tia phân giác của một góc) (1)
Mà \(\widehat {{\rm{yOz}}} + \widehat {{\rm{zOt}}} = \widehat {{\rm{yOt}}}\) (hai góc kề nhau) (2)
Từ (1) và (2) suy ra \(\widehat {{\rm{yOz}}} = \widehat {{\rm{zOt}}} = \frac{{\widehat {{\rm{yOt}}}}}{2} = \frac{{70^\circ }}{2} = 35^\circ \)
Ta có \(\widehat {{\rm{xOy}}} + \widehat {{\rm{yOz}}} = \widehat {{\rm{xOz}}}\) (hai góc kề nhau)
Hay \(110^\circ + 35^\circ = \widehat {{\rm{yOz}}}\)
Suy ra \(\widehat {{\rm{yOz}}} = 145^\circ \)
Vậy ta chọn phương án D.
Câu 3:
Cho hình vẽ
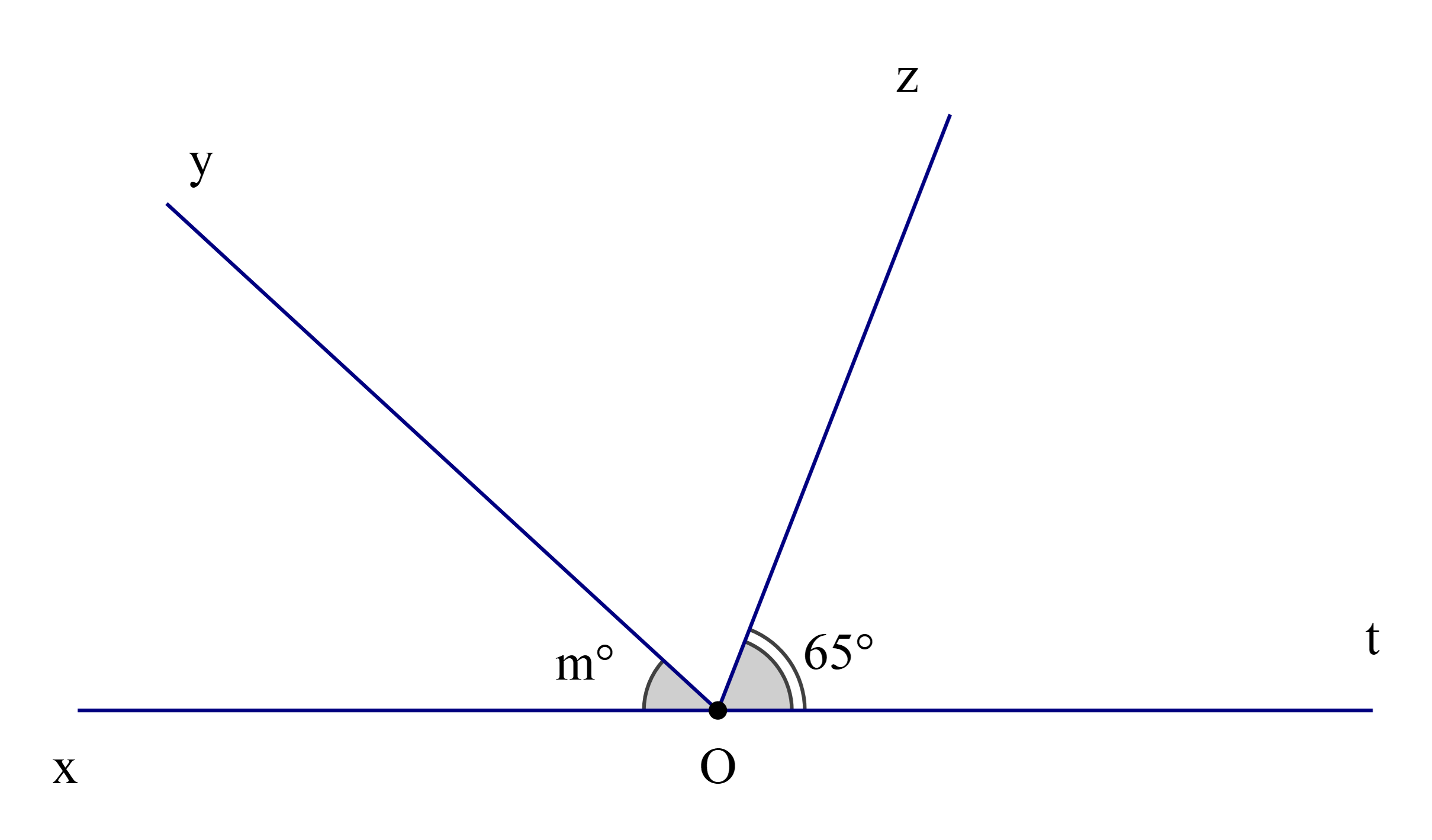
Giá trị của m để tia Oz là tia phân giác của \(\widehat {{\rm{yOt}}}\) là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Để tia Oz là tia phân giác của \(\widehat {{\rm{yOt}}}\) thì \(\widehat {{\rm{yOz}}} = \widehat {{\rm{zOt}}}\) (1)
Mà \(\widehat {{\rm{yOz}}} + \widehat {{\rm{zOt}}} = \widehat {{\rm{yOt}}}\) (hai góc kề nhau) (2)
Từ (1) và (2) suy ra \(\widehat {{\rm{yOz}}} = \widehat {{\rm{zOt}}} = \frac{{\widehat {{\rm{yOt}}}}}{2}\)
Suy ra \(\widehat {{\rm{yOt}}} = 2\widehat {{\rm{zOt}}} = 2.65^\circ = 130^\circ \)
Ta lại có \(\widehat {xOy} + \widehat {{\rm{yOt}}} = 180^\circ \) (hai góc kề bù)
Suy ra \(\widehat {{\rm{xOy}}} = 180^\circ - \widehat {yOt} = 180^\circ - 130^\circ = 50^\circ \)
Do đó m = 50
Vậy ta chọn phương án A.
Câu 4:
Cho hình vẽ:

Biết rằng EF // BC. Số đo của \(\widehat {BEF}\) là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
Theo bài ta có EF // BC (1)
Mà \(\widehat {{\rm{AEF}}}\) và \(\widehat {{\rm{EBC}}}\) là hai góc nằm ở vị trí đồng vị (2)
Từ (1) và (2) suy ra \(\widehat {{\rm{AEF}}} = \widehat {{\rm{EBC}}} = 50^\circ \) (tính chất hai đường thẳng song song).
Lại có \(\widehat {BEF} + \widehat {AEF} = 180^\circ \) (hai góc kề bù)
Suy ra \(\widehat {BEF} = 180^\circ - \widehat {AEF}\)
Hay \(\widehat {BEF} = 180^\circ - 50^\circ = 130^\circ .\)
Vậy ta chọn phương án D.
Câu 5:
Cho hình vẽ. Biết rằng x // y; đường thẳng z cắt hai đường thẳng x, y lần lượt tại A, B sao cho \({\widehat {\rm{A}}_1} = 60^\circ \).
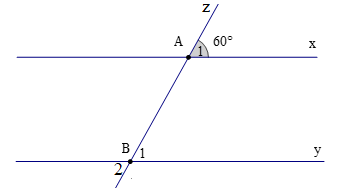
Số đó của \({\widehat {\rm{B}}_2}\) là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Vì x // y nên \({\widehat {\rm{A}}_1}{\rm{ = }}{\widehat {\rm{B}}_1}{\rm{ = 60}}^\circ \) (hai góc đồng vị)
Ta có \({\widehat {\rm{B}}_1} = {\widehat {\rm{B}}_2}\) (hai góc đối đỉnh)
Suy ra \({\widehat {\rm{B}}_2} = 60^\circ \)
Vậy ta chọn phương án A.
Câu 6:
Cho hình vẽ
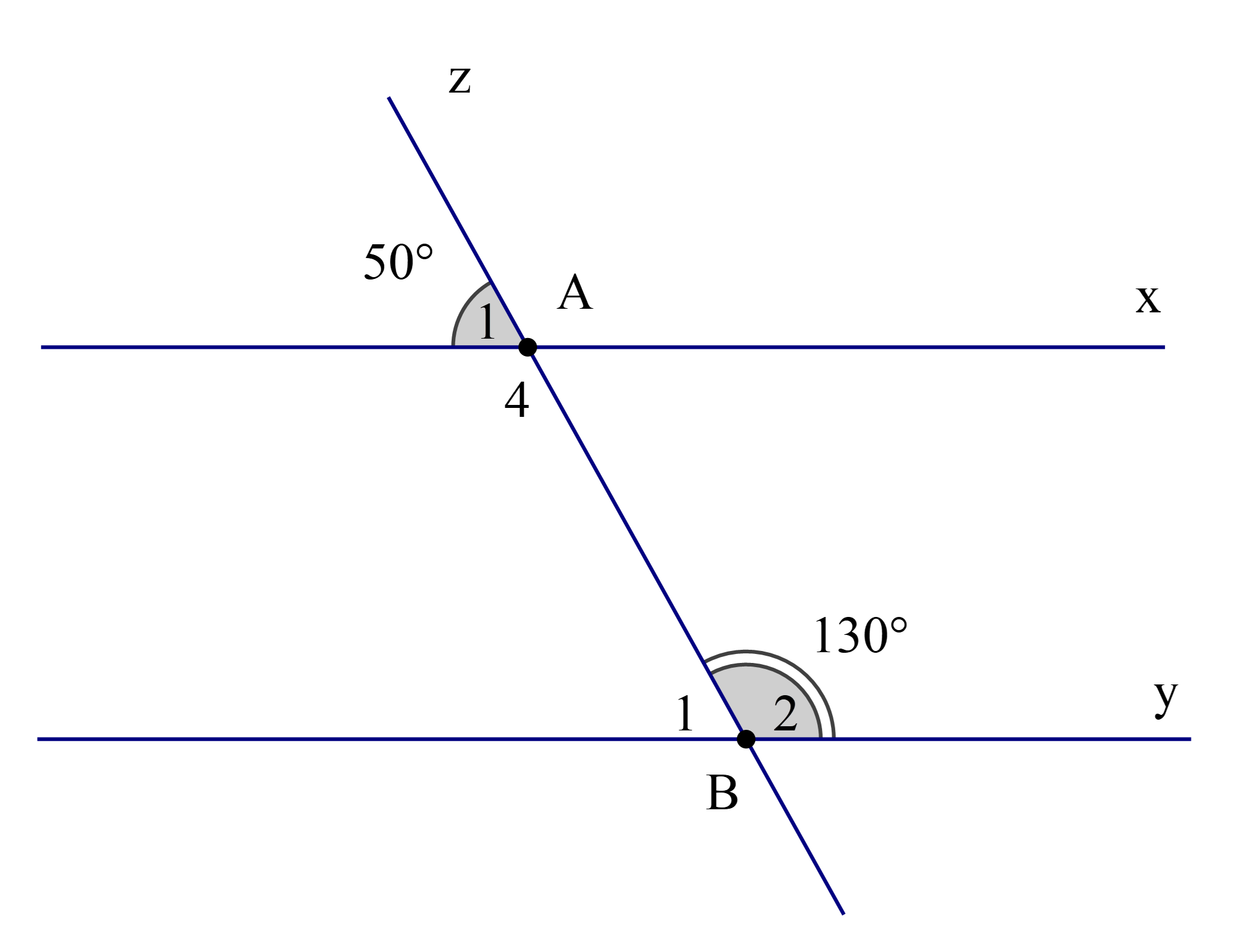
Chọn khẳng định sai:
 Xem đáp án
Xem đáp án
Hướng dẫm giải
Đáp án đúng là: D
Ta có \({\widehat {\rm{B}}_1} + {\widehat {\rm{B}}_1} = 180^\circ \) (hai góc kề bù)
Hay \({\widehat {\rm{B}}_1} + 130^\circ = 180^\circ \)
Suy ra \({\widehat {\rm{B}}_1} = 180^\circ - 130^\circ = 50^\circ \) nên phương án B đúng.
Ta lại có \({\widehat {\rm{A}}_1} + {\widehat {\rm{A}}_4} = 180^\circ \) (hai góc kề bù)
Hay \(50^\circ + {\widehat {\rm{A}}_4} = 180^\circ \)
Suy ra \({\widehat {\rm{A}}_4} = 180^\circ - 50^\circ = 130^\circ \) nên phương án C đúng.
Vì \({\widehat {\rm{A}}_1} = {\widehat {\rm{B}}_1}\) (cùng bằng 50°)
Mà \({\widehat {\rm{A}}_1}\) và \({\widehat {\rm{B}}_1}\) nằm ở vị trí đồng vị
Do đó x // y nên A đúng.
Ta có \(\widehat {xAB} = {\widehat A_1}\) (hai góc đối đỉnh)
Do đó \(\widehat {xAB} = 50^\circ \) nên D sai.
Vậy ta chọn phương án D.
Câu 7:
Cho hình vẽ
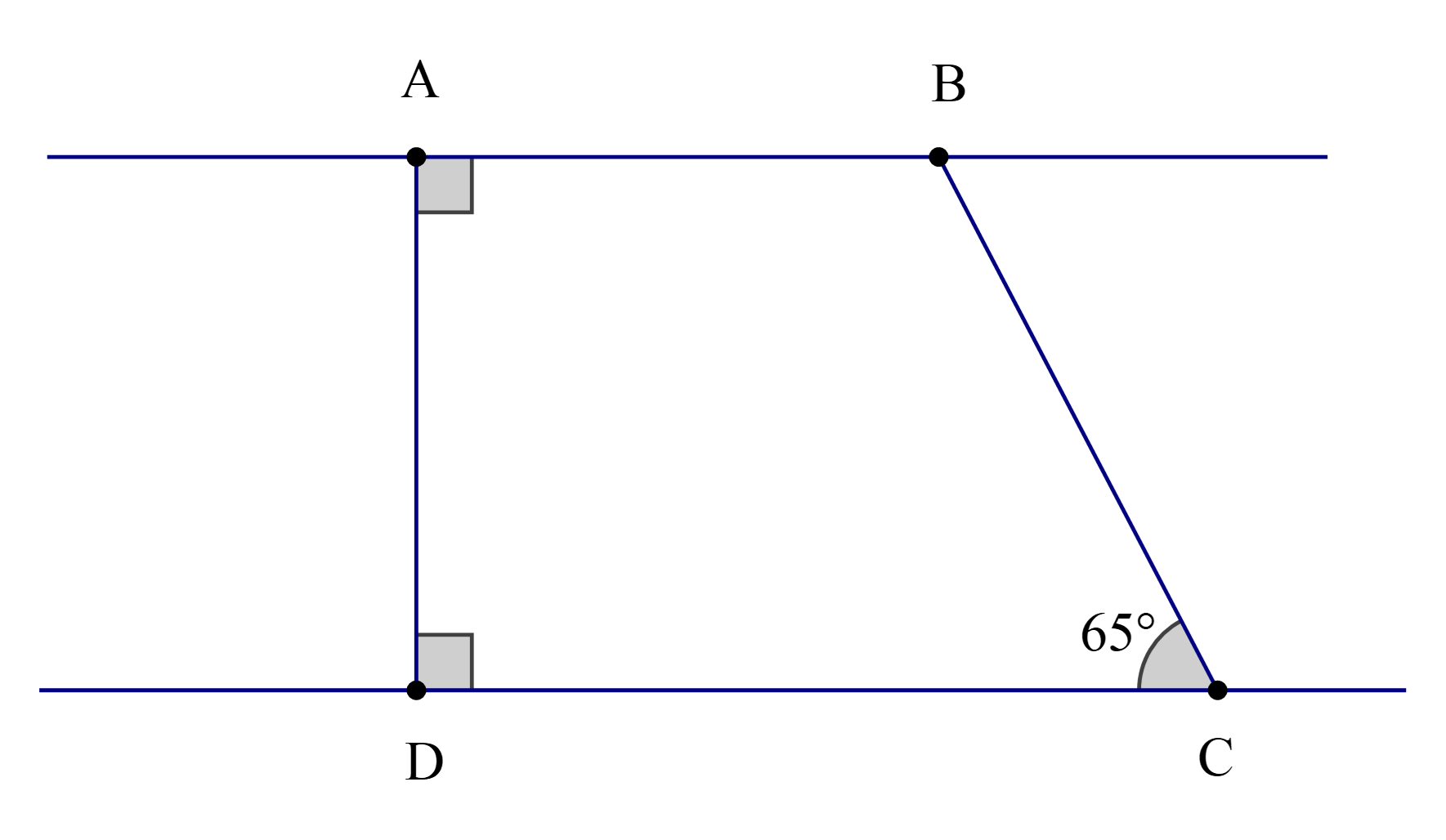
Số đo của \(\widehat {{\rm{ABC}}}\) là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
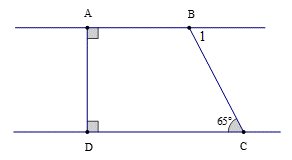
Ta có: AB ⊥ AD và DC ⊥ AD.
Suy ra AB // CD (hai đường thẳng phân biệt cũng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau).
Do đó \(\widehat {DCB} = {\widehat B_1}\) (hai góc so le trong)
Nên \({\widehat B_1} = 65^\circ .\)
Mà \(\widehat {{\rm{ABC}}} + {\widehat {\rm{B}}_1} = 180^\circ \) (hai góc kề bù)
Hay \(\widehat {{\rm{ABC}}} + 65^\circ = 180^\circ \)
Suy ra \(\widehat {{\rm{ABC}}} = 180^\circ - 65^\circ = 115^\circ \)
Vậy ta chọn phương án C.
Câu 8:
Một định lí được minh họa bởi hình vẽ:
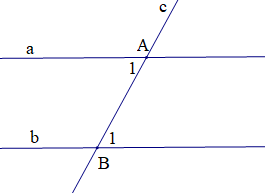
Định lí có giả thiết và kết luận như sau:
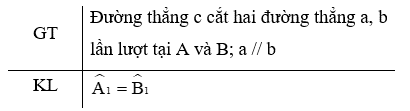
Định lí được phát biểu thành lời là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
Từ giả thiết và kết luận ta có: Nếu đường thẳng c cắt hai đường thẳng song song a và b lần lượt tại hai điểm A và B thì hai góc so le trong \({\widehat A_1}\) và \({\widehat B_1}\) bằng nhau.
Một cách tổng quát ta có định lí: Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc so le trong bằng nhau.
Vậy ta chọn phương án C.
