Cho đường tròn tâm \[O\], các dây \[AB,CD\] vuông góc với nhau. Các tiếp tuyến với đường tròn tại \[A,B,C,D\] cắt nhau lần lượt tại \[E,F,G,H\]. Chứng minh rằng \[EFGH\] là tứ giác nội tiếp.
Giải bởi Vietjack
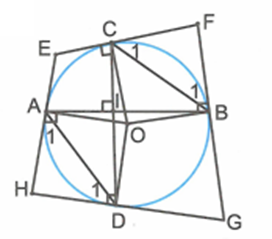
Gọi \[I\] là giao điểm của \[AB\] và \[CD\]. Góc \[\widehat {BIC} = 90^\circ \] và là góc có đỉnh \[I\] ở bên trong đường tròn nên .
Suy ra \[\widehat {{A_1}} + \widehat {{D_1}} + \widehat {{B_1}} + \widehat {{C_1}} = 180^\circ \].
Ta có \[\widehat F + \widehat H = 180^\circ - \left( {\widehat {{C_1}} + \widehat {{B_1}}} \right) + 180^\circ - \left( {\widehat {{A_1}} + \widehat {{D_1}}} \right) = 180^\circ \].
Vậy \[EFGH\] là tứ giác nội tiếp.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho tam giác \[ABC\] vuông tại \[A\]. Đường tròn \[\left( O \right)\] nội tiếp tam giác \[ABC\] tiếp xúc với \[AB,AC\] lần lượt tại \[D,E\].
Tính bán kính của đường tròn \[\left( O \right)\] biết \[AB = 3{\rm{ cm}},AC = 4{\rm{ cm}}\].
Cho đường tròn \[\left( O \right)\] nội tiếp tam giác \[ABC\]. \[D,E,F\] lần lượt là các tiếp điểm \[AB,BC,CA\] với \[\left( O \right)\].
Tìm các hệ thức tương tự hệ thức ở bài trước.
Tứ giác \[ABCD\] ngoại tiếp đường tròn \[\left( O \right)\], đồng thời nội tiếp một đường tròn khác. \[AB = 14{\rm{ cm}},BC = 18{\rm{ cm}},CD = 26{\rm{ cm}}\]. Gọi \[H\] là tiếp điểm của \[CD\] và đường tròn \[\left( O \right)\]. Tính các độ dài \[HC,HD\].
Chứng minh định lí: “Nếu một tứ giác \[ABCD\] có tổng các cạnh đối bằng nhau \[AB + CD = BC + AD\] thì tứ giác đó ngoại tiếp được một đường tròn” bằng cách chứng minh các tia phân giác của bốn góc \[A,B,C,D\] cùng gặp nhau tại một điểm.
Cho tam giác \[ABC\] vuông tại \[A\]. Đường tròn \[\left( O \right)\] nội tiếp tam giác \[ABC\] tiếp xúc với \[AB,AC\] lần lượt tại \[D,E\].
Tứ giác \[ADOE\] là hình gì? Vì sao?
Cho đường tròn \[\left( O \right)\] nội tiếp tam giác \[ABC\]. \[D,E,F\] lần lượt là các tiếp điểm \[AB,BC,CA\] với \[\left( O \right)\].
Chứng minh rằng \[2AD = AB + AC - BC\].
