Cho hình chóp S.ABCD đáy là hình vuông cạnh a, mặt bên (SAB), (SAD) vuông góc với đáy, các mặt bên (SBC), (SCD) cùng tạo với đáy góc 60°.
a) Chứng minh rằng
 Giải bởi Vietjack
Giải bởi Vietjack
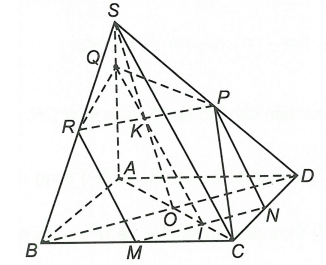
Hai mặt phẳng (SAB), (SAD) cùng vuông góc với mặt đáy nên có giao tuyến SA cũng vuông góc mặt đáy.
a) Ta có
Tương tự
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh 2a, và . Gọi M là trung điểm của BC, khi đó khoảng cách từ A đến đường thẳng SM bằng
c) Viết phương trình tiếp tuyến song song với trục hoành của đồ thị hàm số .
Cho chuyển động thẳng xác định bởi phương trình , trong đó t được tính bằng giây và S được tính bằng mét. Vận tốc của chuyển động tại thời điểm t=2s là
Cho hình chóp S.ABC có và , gọi I là trung điểm BC. Góc giữa hai mặt phẳng và (ABC) là góc nào sau đây?
Cho hình chóp S.ABCD có đáy ABCD là hình vuông, . Mặt phẳng qua A và vuông góc với SC cắt SB, SC, SD theo thứ tự tại H, M, K. Chọn khẳng định sai trong các khẳng định sau.