Cho biểu thức:
a) Tìm điều kiện xác định của biểu thức P.
b) Chứng minh giá trị của P luôn âm với x ≠ ±1
 Giải bởi Vietjack
Giải bởi Vietjack
a) Ta có: x4 - 1 = (x2 + 1)(x2-1), trong đó : x2 + 1 > 0, với mọi x.
Vậy điều kiện : x2 – 1 ≠ 0
x2 – 1 = (x – 1)(x + 1) ≠ 0 ⇒ x ≠ ±1
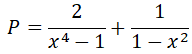
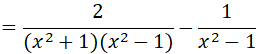
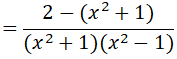
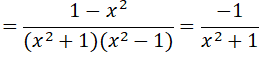
Do x2 + 1 > 0 với mọi x nên P < 0 với mọi x ≠ ±1
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho tam giác ABC vuông tại A. Gọi M, N lần lượt là trung điểm của hai cạnh AB và BC.
a) Gọi D là điểm đối cứng của A qua N. Chứng minh tứ giác ABCD là hình chữ nhật.
b) Lấy I là trung điểm của cạnh AC và E là điểm đối xứng của N qua I.
Chứng minh tứ giác ANCE là hình thoi.
c) Đường thẳng BC cắt DM và DI lần lượt tại G và G’. Chứng minh BG = CG’.
d) Cho AB = 6cm, AC = 8cm. Tính diện tích ΔDGG’.