 Giải bởi Vietjack
Giải bởi Vietjack
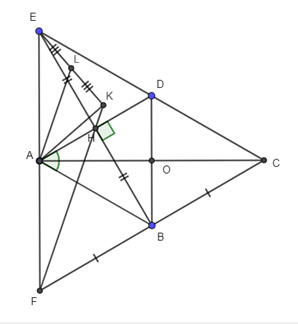
a) Xét tam giác ABD có AB = AD (do ABCD là hình thoi)
Suy ra tam giác ABD cân
Mà nên tam giác ABD đều
Ta lại có BH là đường cao nên BH cũng là đường trung tuyến của
suy ra H là trung điểm của AD.
Xét tứ giác ABDE có hai đường chéo AD và BE cắt nhau tại H
H là trung điểm của BE (do B và E đối xứng với nhau qua H)
H là trung điểm của AD (cmt)
Do đó ABDE là hình bình hành
Mà tại H (gt).
suy ra ABDE là hình thoi.b. Ta có DE//AB (ABDE là hình thoi) và DC//AB (ABCD là hình thoi) nên ED, DC trùng nhau
suy ra E,D,C thẳng hàng
Xét tứ giác ABCE có AB // DE nên tứ giác ABCE là hình thang (1)
Ta có: (hai góc đối trong hình thoi ABCD)
Do tam giác ABD đều nên AB = BD = AD = AE = DE
Suy ra tam giác AED đều
(2)
Từ (1) và (2) suy ra ABCE là hình thang cân.c. Vì ABCD là hình thoi có hai đường chéo AC giao BD tại O nên O là trung điểm của AC
Xét tam giác ACF có:
O là trung điểm của AC (cmt)
B là trung điểm của CF (C và F đối xứng với nhau qua B)
Suy ra OB là đường trung bình của tam giác ACF.
suy ra OB // AF
Mà BD // AE (ABDE là hình thoi)
Do đó AF trùng với AE hay A, F, E thẳng hàng.
Xét tam giác CFE, có :
D là trung điểm của CE
AD // EF
Suy ra A là trung điểm của EF.
Xét tam giác KFE, có :
L là trung điểm của KE (gt)
A là trung điểm của EF (cmt)
Suy ra AL là đường trung bình của tam giác FKE.
Suy ra AL//FKGói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho
a) Rút gọn biểu thức A.
b) Tính giá trị của biểu thức A biết x2 = 9.
c) Tìm giá trị nhỏ nhất của B biết B = A.(x2 – 5x + 4).
Tìm tất cả các tam giác vuông có số đo các cạnh là các số nguyên dương và số đo diện tích bằng số đo chu vi.
Tìm đa thức thương và đa thức dư trong phép chia sau:
(2x3 – 7x2 + 13x + 2) : (2x – 1).
b) Xác định số hữu tỉ a để f(x) = x3 – 2x2 + 5x + a chia hết cho đa thức g(x) = x – 3.