Cho tam giác ABC, phân giác BD. Đường trung trực của BD cắt đường thẳng AC tại E.
a) Chứng minh ΔBED cân
b) Chứng minh ΔEAB và ΔEBC đồng dạng
c) Tính độ dài ED biết
 Giải bởi Vietjack
Giải bởi Vietjack
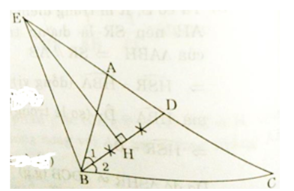
a) Do EH là đường trung trực của BD nên ΔBED có đường cao EH đồng thời là đường trung tuyến.
∠ ΔBED cân tại E.
b)Ta có: ∠EBD = ∠EDB (ΔBED cân)
mà ∠B1 = ∠B2 (gt)
và ∠EBC = ∠EBD + ∠B2
∠EAB = ∠EDB + ∠B1 (góc ngoài ΔABD)
Do đó: ∠EAB = ∠EBC (1)
Xét ΔEAB và ΔEBC có
∠E chung
∠EAB = ∠EBC (cmt)
∠ ΔEAB ∼ ΔEBC (g.g)
c)Ta có ΔEAB ∼ ΔEBC (cmt)
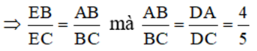
![]()
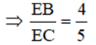
∠ 5EB = 4EC ∠ 5EB = 4(EB + DC) vì EB = ED
∠ 5EB = 4(EB + 5) ∠ EB = 20 (cm)
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho tam giác ABC vuông tại A có ∠B = 2∠C, đường cao AD.
a) Chứng tỏ ΔADB và ΔCAB đồng dạng
b) Kẻ tia phân giác của góc ABC cắt AD tại F và AC tại E
Chứng tỏ AB2 = AE.AC
c) Chứng tỏ
d) Biết AB = 2BD. Chứng tỏ diện tích tam giác ABC bằng ba lần diện tích tam giác BFC.
Cho ΔABC và ΔMNP đồng dạng với nhau theo tỉ số đồng dạng k = 3/2 . Chu vi tam giác ABC bằng 36cm. Chu vi tam giác MNP là:
Cho hình bình hành ABCD, biết Trên cạnh AB lấy E sao cho AE = 8cm. Đường thẳng DE cắt BC tại F. Độ dài BF là:
Cho tam giác ABC vuông tại A, đường cao AH chia cạnh huyền thành hai đoạn thẳng có độ dài 4cm và 9cm. Diện tích tam giác vuông đó là:
Cho ΔABC, một đường thẳng a song song với BC cắt AB, AC theo thứ tự tại M và N. Khi đó:
Gọi M là điểm nằm trên đoạn thẳng PQ sao cho . Tỉ số là:
Cho hình thang ABCD Gọi O là giao điểm hai đường chéo AC và BD. Đường thẳng qua O và song song với hai đáy cắt AD tại E. Biết Tỉ số đồng dạng của hai tam giác AOE và ACD là: