Với giá trị của x thỏa mãn thì
A. 20
B. 30
C. -10
D. 34
 Giải bởi Vietjack
Giải bởi Vietjack
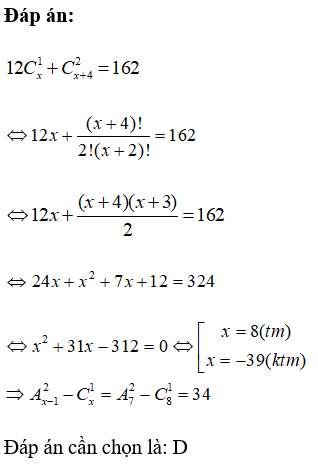
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Từ 7 chữ số 1,2,3,4,5,6,7 có thể lập được bao nhiêu số từ 4 chữ số khác nhau?
Số tam giác xác định bởi các đỉnh của một đa giác đều 10 cạnh là:
Một lớp có 40 học sinh. Số cách chọn ra 5 bạn để làm trực nhật là:
Số các véc tơ (khác ) được tạo thành từ 10 điểm phân biệt trong mặt phẳng là:
Một lớp có 8 học sinh được bầu chọn vào 3 chức vụ khác nhau: lớp trưởng, lớp phó và bí thư (không được kiêm nhiệm). Số cách lựa chọn khác nhau sẽ là:
Dũng có 8 người bạn. Dũng muốn mời 4 trong 8 người bạn đó về quê chơi vào cuối tuần. Nhưng trong 8 người bạn đó, có 2 bạn là Hùng và Tuấn không thích đi chơi với nhau. Như vậy số cách chọn nhóm 4 người để về quê của Dũng là?
Chọn công thức KHÔNG đúng khi tính số chỉnh hợp chập k của n phần tử.
Trong một hộp bánh có 6 loại bánh nhân thịt và 4 loại bánh nhân đậu xanh. Có bao nhiêu cách lấy ra 6 bánh để phát cho các em thiếu nhi.
Có bao nhiêu số có 5 chữ số đôi một khác nhau tạo thành từ các chữ số 1,2,3,4,5 ?
Trong một bình đựng 4 viên bi đỏ và 3 viên bi xanh. Lấy ngẫu nhiên ra 2 viên. Có bao nhiêu cách lấy được 2 viên cùng màu?
Cho tập A có 26 phần tử. Hỏi A có bao nhiêu tập con gồm 6 phần tử?
Cho tập A={1;2;4;6;7;9}. Hỏi có thể lập được từ tập A bao nhiêu số tự nhiên có 4 chữ số đôi một khác nhau, trong đó không có mặt chữ số 7.
Từ các chữ số 1;2;3;......;9 lập được bao nhiêu số có 3 chữ số đôi một khác nhau.
I. Hoán vị
1. Định nghĩa
- Định nghĩa: Cho tập hợp A gồm n phần tử (n ≥ 1). Mỗi kết quả của sự sắp xếp thứ tự n phần tử của tập hợp A được gọi là một hoán vị của n phần tử đó.
- Nhận xét: Hai hoán vị của n phần tử khác nhau ở thứ tự sắp xếp.
Chẳng hạn, hai hoán vị abc và cab của ba phần tử a; b; c là khác nhau.
2. Số các hoán vị
Kí hiệu: Pn là số các hoán vị của n phần tử.
- Định lí: Pn = n.(n – 1).(n – 2)….2.1
- Chú ý: Kí hiệu n.(n – 1)…2.1 là n! (đọc là n là giai thừa), ta có: Pn = n!.
- Ví dụ 1. Có bao nhiêu cách xếp 10 học sinh thành một hàng ngang.
Lời giải:
Số cách xếp 10 học sinh thành một hàng ngang là 10! cách.
II. Chỉnh hợp
1. Định nghĩa.
- Cho tập hợp A gồm n phần tử (n ≥ 1).
Kết quả của việc lấy k phần tử khác nhau từ n phần tử của tập hợp A và sắp xếp chúng theo một thứ tự nào đó được gọi là một chỉnh hợp chập k của n phần tử đã cho.
- Ví dụ 2. Lớp 11A2 có 40 học sinh. Khi đó; mỗi cách chọn ra 4 bạn làm tổ trưởng tổ 1; tổ 2; tổ 3; tổ 4 chính là số chỉnh hợp chập 4 của 40 học sinh.
2. Số các chỉnh hợp
- Kí hiệu là số các chỉnh hợp chập k của n phần tử (1 ≤ k ≤ n) .
- Định lí:
- Ví dụ 3. Từ năm điểm phần biệt A; B; C; D; E ta lập được bao nhiêu vectơ khác có điểm đầu và điểm cuối là năm điểm đã cho.
Lời giải:
Một vectơ được xác định khi biết điểm đầu và điểm cuối của nó.
Số vecto khác có điểm đầu và điểm cuối là năm điểm đã cho chính là chỉnh hợp chập 2 của 5 phần tử:
Do đó, ta có: vectơ thỏa mãn đầu bài.
- Chú ý:
a) Với quy ước 0! = 1 ta có: .
b) Mỗi hoán vị của n phần tử cũng chính là một chỉnh hợp chập n của n phần tử đó.
Vì vậy: .
III. Tổ hợp
1. Định nghĩa.
- Giả sử tập A có n phần tử (n ≥ 1). Mỗi tập con gồm k phần tử của A được gọi là một tổ hợp chập k của n phần tử đã cho.
- Chú ý: Số k trong định nghĩa cần thỏa mãn điều kiện 1 ≤ k ≤ n. Tuy vậy, tập hợp không có phần tử nào là tập rỗng nên ta quy ước gọi tổ hợp chập 0 của n phần tử là tập rỗng.
- Ví dụ 4. Cho tập A = {3; 4; 5; 6}.
Ta liệt kê các tổ hợp chập 3 của A là: {3; 4; 5}; {3; 4; 6}; {3; 5; 6}; {4; 5; 6}.
2. Số các tổ hợp.
Kí hiệu là số các tổ hợp chập k của n phần tử ( 0 ≤ k ≤ n).
- Định lí: .
Ví dụ 5. Cho 8 điểm phân biệt A; B; C; D; E; F; G; H, trong đó không có 3 điểm nào thẳng hàng, ta lập được bao nhiêu tam giác có 3 đỉnh là 8 điểm đã cho.
Lời giải:
Mỗi tam giác được lập là 1 tổ hợp chập 3 của 8 (điểm).
Vì vậy số tam giác có 3 đỉnh là 8 điểm đã cho là 56.
3. Tính chất của các số
a) Tính chất 1.
.
Ví dụ 6. .
b) Tính chất 2 (công thức Pa-xcan).
Ví dụ 7. .