Tìm trong thực tiễn các hình ảnh vẽ điểm, đường thẳng, đoạn thẳng, trung điểm của đoạn thẳng, tia, góc.
 Giải bởi Vietjack
Giải bởi Vietjack
Các hình ảnh trong thực tiễn về điểm, đường thẳng, đoan thẳng, trung điểm của đoạn thẳng, tia và góc.
- Các ngôi sao trên trời thường được coi là những điểm trên trời.

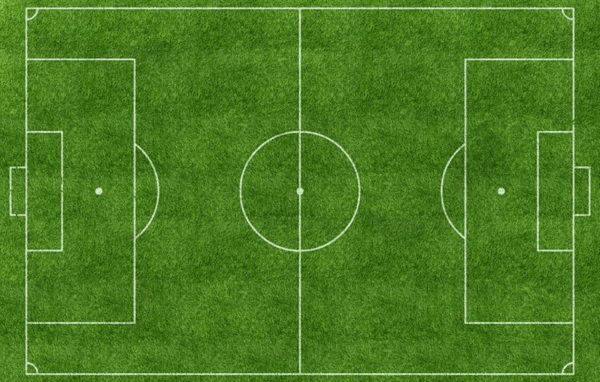
- Con đường thẳng cũng được coi là hình ảnh của một đường thẳng trong thực tế:

- Thanh gỗ là hình ảnh thực tế của một đoạn thẳng:

- Trung điểm của đoạn thẳng
- Các tia sáng mặt trời là hình ảnh của tia:

- Góc giữa hai mái nhà của ngôi nhà:

Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Trên đường thẳng xy lấy một điểm O. Trên tia Ox lấy điểm A sao cho OA = 3 cm. Trên tia Oy lấy hai điểm B và C sao cho OB = 3 cm và OC = a (cm), với 0 < a < 3.
a) Điểm O có là trung điểm của đoạn thẳng AB không? Vì sao?
b) Xác định giá trị của a để C là trung điểm của đoạn thẳng OB.
Cho góc xOy = 900 và điểm M nằm trong góc đó. Góc xOM là góc nhọn hay góc tù?
Dùng thước đo góc để đo các góc tại đỉnh của ngôi sao, mặt thớt gỗ ở hình dưới đây.

Quan sát Hình 96.
a) Đọc tên bốn cặp tia đối nhau.
b) Đọc tên bốn cặp tia trùng nhau.

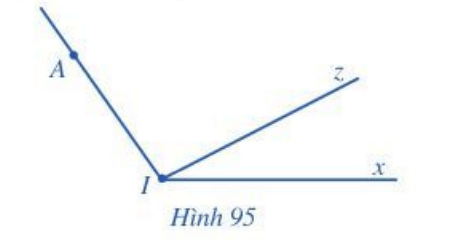
Quan sát Hình 95.
a) Đọc tên các tia có trong hình.
b) Đọc tên các góc có trong hình.
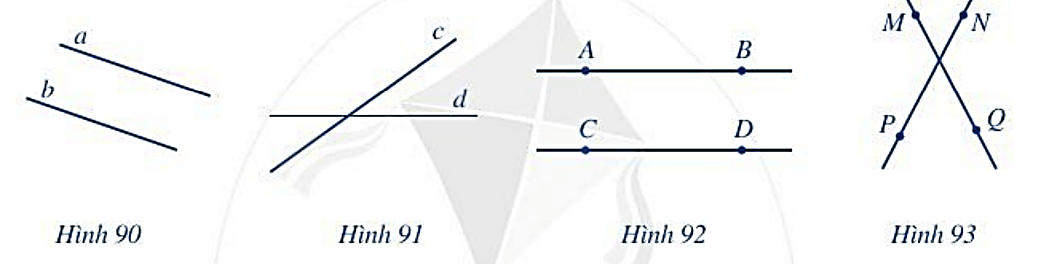
Đọc tên hai đường thẳng song song, hai đường thẳng cắt nhau trong Hình 90, Hình 91, Hình 93, Hình 94
a) Đọc tên điểm, đường thẳng, đoạn thẳng trong Hình 89.

b) Vẽ hai điểm M, N và đường thẳng đi qua hai điểm đó.
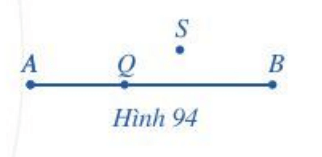
a) Đọc tên ba điểm thẳng hàng và điểm nằm giữa hai điểm còn lại trong Hình 94.
b) Đọc tên ba điểm không thẳng hàng trong Hình 94.
c) Vẽ ba điểm A, B, C thẳng hàng.
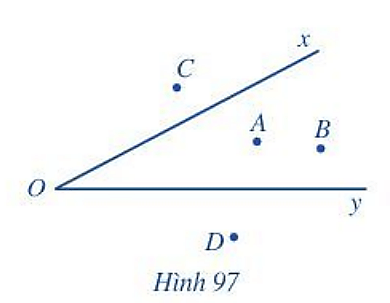
Trong Hình 97, đọc tên các điểm:
a) Nằm trong góc xOy;
b) Nằm ngoài góc xOy.
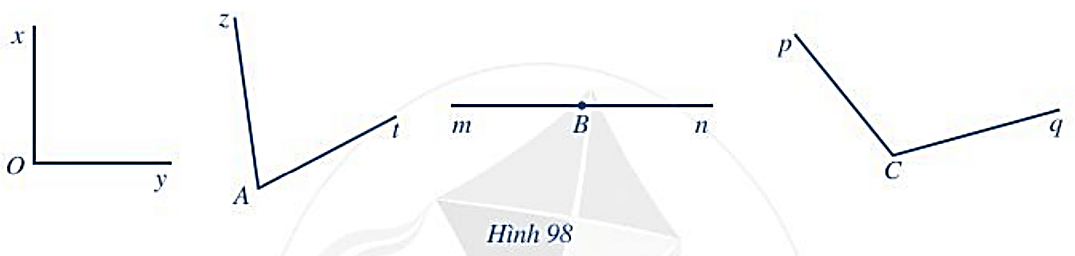
Đo các góc trong Hình 98 và chỉ ra góc nhọn, góc vuông, góc tù, góc bẹt.
Chọn từ “nhọn”, "vuông”, "tù", "bẹt" thích hợp cho ( ? )
a) Nếu thì góc xOy là góc ( ? );
b) Nếu thì góc mIn là góc ( ? );
c) Nếu thì góc uHv là góc ( ? );
d) Nếu thì góc zKt là góc ( ? ).



Một hộp có 5 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, 4, 5; hai thẻ khác nhau thì ghi số khác nhau. Rút ngẫu nhiên một thẻ rồi bỏ lại thẻ vào hộp.
Sau 25 lần rút thẻ liên tiếp, hãy ghi kết quả thống kê theo mẫu sau:
|
Lần 1 |
Số 3 |
Lần 6 |
Số 5 |
Lần 11 |
Số 3 |
Lần 16 |
Số 2 |
Lần 21 |
Số 1 |
|
Lần 2 |
Số 1 |
Lần 7 |
Số 2 |
Lần 12 |
Số 2 |
Lần 17 |
Số 1 |
Lần 22 |
Số 5 |
|
Lần 3 |
Số 2 |
Lần 8 |
Số 3 |
Lần 13 |
Số 2 |
Lần 18 |
Số 2 |
Lần 23 |
Số 3 |
|
Lần 4 |
Số 3 |
Lần 9 |
Số 4 |
Lần 14 |
Số 1 |
Lần 19 |
Số 3 |
Lần 24 |
Số 4 |
|
Lần 5 |
Số 4 |
Lần 10 |
Số 5 |
Lần 15 |
Số 5 |
Lần 20 |
Số 5 |
Lần 25 |
Số 5 |
Tính xác suất thực nghiệm
Xuất hiện số chẵn

Một hộp có 5 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, 4, 5; hai thẻ khác nhau thì ghi số khác nhau. Rút ngẫu nhiên một thẻ rồi bỏ lại thẻ vào hộp.
Sau 25 lần rút thẻ liên tiếp, hãy ghi kết quả thống kê theo mẫu sau:
|
Lần 1 |
Số 3 |
Lần 6 |
Số 5 |
Lần 11 |
Số 3 |
Lần 16 |
Số 2 |
Lần 21 |
Số 1 |
|
Lần 2 |
Số 1 |
Lần 7 |
Số 2 |
Lần 12 |
Số 2 |
Lần 17 |
Số 1 |
Lần 22 |
Số 5 |
|
Lần 3 |
Số 2 |
Lần 8 |
Số 3 |
Lần 13 |
Số 2 |
Lần 18 |
Số 2 |
Lần 23 |
Số 3 |
|
Lần 4 |
Số 3 |
Lần 9 |
Số 4 |
Lần 14 |
Số 1 |
Lần 19 |
Số 3 |
Lần 24 |
Số 4 |
|
Lần 5 |
Số 4 |
Lần 10 |
Số 5 |
Lần 15 |
Số 5 |
Lần 20 |
Số 5 |
Lần 25 |
Số 5 |
Tính xác suất thực nghiệm
Xuất hiện số 2

Một hộp có 5 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, 4, 5; hai thẻ khác nhau thì ghi số khác nhau. Rút ngẫu nhiên một thẻ rồi bỏ lại thẻ vào hộp.
Sau 25 lần rút thẻ liên tiếp, hãy ghi kết quả thống kê theo mẫu sau:
|
Lần 1 |
Số 3 |
Lần 6 |
Số 5 |
Lần 11 |
Số 3 |
Lần 16 |
Số 2 |
Lần 21 |
Số 1 |
|
Lần 2 |
Số 1 |
Lần 7 |
Số 2 |
Lần 12 |
Số 2 |
Lần 17 |
Số 1 |
Lần 22 |
Số 5 |
|
Lần 3 |
Số 2 |
Lần 8 |
Số 3 |
Lần 13 |
Số 2 |
Lần 18 |
Số 2 |
Lần 23 |
Số 3 |
|
Lần 4 |
Số 3 |
Lần 9 |
Số 4 |
Lần 14 |
Số 1 |
Lần 19 |
Số 3 |
Lần 24 |
Số 4 |
|
Lần 5 |
Số 4 |
Lần 10 |
Số 5 |
Lần 15 |
Số 5 |
Lần 20 |
Số 5 |
Lần 25 |
Số 5 |
Tính xác suất thực nghiệm
Xuất hiện số 1




