Cách tính thể tích của các hình lớp 5 chi tiết
Hamchoi.vn giới thiệu 50 bài tập Cách tính thể tích của các hình lớp 5 chi tiết lớp 5 gồm các dạng bài tập có phương pháp giải chi tiết và các bài tập điển hình từ cơ bản đến nâng cao giúp học sinh biết cách làm. Bên cạnh có là 28 bài tập vận dụng để học sinh ôn luyện dạng Toán 5 này.
Cách tính thể tích của các hình lớp 5 chi tiết
I/ Lý thuyết
- Thể tích của một vật là lượng không gian mà vật ấy chiếm.
- Phân biệt thể tích với dung tích: Dung tích là khả năng chứa đựng tối đa của một vật nào đó.
- Đơn vị đo thể tích tiêu chuẩn là mét khối (kí hiệu: m3 ) hoặc là lít (kí hiệu: l). Ngoài ra còn có những đơn vị nhỏ như cm3 , dm3 hoặc ml.
Đổi: 1m3 = 1000 dm3 = 1000 000 cm3 (Mỗi một đơn vị đo thể tích liền kề hơn kém nhau 1000 lần)
II/ Các dạng bài tập
II.1/ Dạng 1: Tính thể tích của hình hộp chữ nhật
1. Phương pháp giải
- Muốn tính thể tích của hình hộp chữ nhật ta lấy chiều dài nhân với chiều rộng rồi nhân với chiều cao (cùng một đơn vị đo)
- Công thức tính thể tích hình hộp chữ nhật: V = a x b x c
(V là thể tích của hình hộp chữ nhật; a, b, c là ba kích thước của hình hộp chữ nhật)
2. Bài tập minh họa
Bài 1: Tính thể tích của hình hộp chữ nhật có chiều dài 5cm, chiều rộng 3,5cm, chiều cao 3cm.
Thể tích của hình hộp chữ nhật là: 5 x 3,5 x 3 = 52,5 (cm3 )
Đáp số: 52,5 cm3
Bài 2: Một bể nước hình hộp chữ nhật có chiều dài 1,2m, chiều rộng 0,8m, chiều cao 1m. Mực nước trong bể cao 40cm. Sau khi thả hòn non bộ vào thì mực nước trong bể cao 55cm. Tính thể tích hòn non bộ.
Hướng dẫn giải
Thể tích của hòn non bộ chính bằng thể tích của hình hộp chữ nhật có chiều dài và chiều rộng bằng chiều dài và chiều rộng của bể, chiều cao bằng mức nước dâng lên trong bể so với ban đầu.
Đổi: 1,2m = 120cm; 0,8m = 80cm
Phần nước dâng lên số xăng-ti-mét là:
55 – 40 = 15 (cm)
Thể tích của hòn non bộ là:
120 x 80 x 15 = 144 000 (cm3 ) = 144 dm3
Đáp số: 144 dm3
II.2/ Dạng 2: Tính thể tích hình lập phương
1. Phương pháp giải
- Muốn tính thể tích hình lập phương ta lấy cạnh nhân với cạnh rồi nhân với cạnh.
- Công thức tính thể tích hình lập phương: V = a x a x a
(V là thể tích hình lập phương, a là độ dài cạnh hình lập phương)
2. Bài tập minh họa
Bài 1: Tính thể tích hình lập phương có cạnh dài 1,5m.
Hướng dẫn giải
Thể tích của hình lập phương là:
1,5 x 1,5 x 1,5 = 3,375 (m3 )
Đáp số: 3,375 m3
Bài 2: Một khối kim loại hình lập phương có cạnh 1m. Mỗi đề-xi-mét khối kim loại đó có cân nặng là 10kg. Hỏi khối kim loại đó cân nặng bao nhiêu tấn?
Hướng dẫn giải
Thể tích của khối kim loại là:
1 x 1 x 1 = 1 (m3 ) = 1000 dm3
Khối kim loại đó có số cân nặng là:
1000 x 10 = 10 000 (kg) = 10 tấn
Đáp số: 10 tấn
III/ Bài tập vận dụng
Bài 1: Tính thể tích hình hộp chữ nhật có
a, Chiều dài 6,5m; chiều rộng 4m; chiều cao 4,5m
b, Chiều dài 25cm, chiều rộng 2dm, chiều cao 3dm
Bài 2: Tính thể tích hình lập phương có cạnh lần lượt là 7dm; 4,3cm; 2,4m
Bài 3: Một hình lập phương có cạnh 3,5cm. Tính diện tích xung quanh, diện tích toàn phần và thể tích của hình lập phương đó.
Bài 4: Một hình hộp chữ nhật có chiều dài 8cm, chiều rộng 5cm, chiều cao 5cm. Một hình lập phương có cạnh bằng trung bình cộng của 3 kích thước hình hộp chữ nhật trên. Tính thể tích của hình hộp chữ nhật và hình lập phương.
(Áp dụng cách tìm trung bình cộng của các số tìm cạnh hình lập phương. Sau đó tính thể tích hình lập phương và hình hộp chữ nhật)
Bài 5: Một khối gỗ dạng hình hộp chữ nhật có chiều dài 1,2m, chiều rộng 1m, chiều cao 50cm. Người ta cắt đi một phần khối gỗ có dạng hình lập phương cạnh 30cm. Tính thể tích khối gỗ còn lại.
(Tính thể tích hình hộp chữ nhật và thể tích hình lập phương đã cắt đi. Tính thể tích khối gỗ còn lại lấy thể tích hình hộp chữ nhật trừ đi thể tích hình lập phương)
Bài 6: Biết tỉ số thể tích của hai hình lập phương là 3:4. Tính thể tích của hình lập phương lớn biết thể tích của hình lập phương bé là 60 cm3
(Thể tích hình lập phương lớn bằng thể tích hình lập phương nhỏ. Áp dụng tìm phân số của một để tìm thể tích hình lập phương lớn)
Bài 7: Tính thể tích của một hình hộp chữ nhật có diện tích xung quanh bằng 448 cm2, chiều cao 8 cm, chiều dài hơn chiều rộng 4 cm.
(Dựa vào diện tích xung quanh ta tính được tổng chiều dài và chiều rộng. Áp dụng dạng toán tổng hiệu ta tính được chiều dài và chiều rộng hình hộp chữ nhật. Cuối cùng ta tính thể tích hình)
Bài 8: Một hình lập phương có diện tích toàn phần là 294 cm². Hỏi hình lập phương đó có thể tích bao nhiêu?
(Dựa vào diện tích toàn phần chúng ta tính được diện tích mặt đáy của hình lập phương. Dựa vào diện tích mặt đáy ta tìm độ dài 1 cạnh. Cuối cùng tính thể tích của hình)
Bài 9: Một bể cá cảnh hình hộp chữ nhật có chiều 1,2m, chiều rộng 0,4m và chiều cao 0,6m. Mực nước trong bể cao 35cm. Sau khi thả hòn Non Bộ vào trong bể thì mực nước trong bể cao 47cm. Tính thể tích hòn Non Bộ.
(Xem lại phần bài tập minh họa)
Bài 10: Một bể cá dạng hình hộp chữ nhật làm bằng kính ( không có nắp) có chiều dài 80cm, chiều rộng 50cm, chiều cao 45cm. Mực nước ban đầu trong bể cao 35cm.
a) Tính diện tích kính dùng để làm bể cá đó.
b) Người ta cho vào bể một hòn đá có thể tích 10dm3. Hỏi mực nước trong bể lúc này cao bao nhiêu xăng – ti-mét?
(Phần b: Thể tích hòn đá chính bằng thể tích của hình chữ nhật có chiều dài và chiều rộng là chiều dài và chiều rộng của bể cá, chiều cao là độ dài mực nước biển dâng lên. Ta tính độ dài mực nước biển dâng lên. Sau đó ta tính mực nước trong bể cao bao nhiêu xăng-ti-mét)
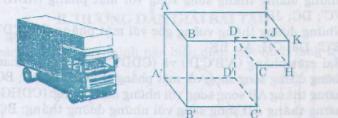
Bài 11: Thùng chứa của một xe chở hàng đông lạnh có dạng như hình 36. Một số mặt là những hình chữ nhật, chẳng hạn (ABKI), (DCC’D’)
– Quan sát hình và trả lời câu hỏi sau:
a) Những đường thẳng nào song song với mặt phẳng (ABKI)
b) Những đường thẳng nào vuông góc với mặt phẳng (DCC’D’)
c) Mặt phẳng (A’D’C’D’) có vuông góc với mặt phẳng (DCC’D’) hay không?
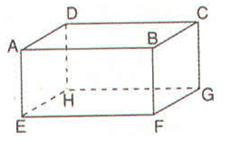
Bài 12: Cho hình hộp chữ nhật ABCD.EFGH
a) Kể tên các đường thẳng song song với mp (EFGH)
b) Đường thẳng AB song song với những mặt phẳng nào?
c) Đường thẳng AD song song với những đường thẳng nào?
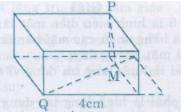
Bài 13: Đố: Các kích thước của một hình hộp chữ nhật là 4cm, 3cm, 2cm. Một con kiến bò theo mặt của hình hộp đó từ Q đến P
a) Hỏi con kiến bò theo đường nào là ngắn nhất?
b) Độ dài ngắn nhất đó bằng bao nhiêu xentimet?
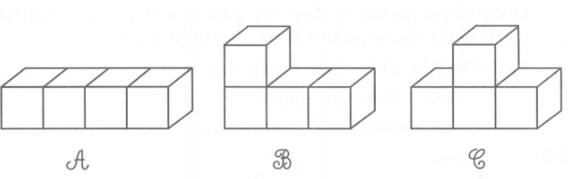
Bài 14: Tính thể tích các hình sau biết mỗi cạnh 1cm:
Bài 15:
Một bể cá dạng hình hộp chữ nhật làm bằng kính (không có nắp) có chiều dài 80 cm, chiều rộng 50 cm, chiều cao 45 cm.
Mực nước ban đầu trong bể cao 35 cm.
a) Tính diên tích kính dùng để làm bể cá đó.
b) Người ta cho vào bể một hòn đá có thể tích 10 dm3. Hỏi mực nước trong bể lúc này cao bao nhiêu xăng – ti-mét?
Bài 16: Tính thể tích hình sau:
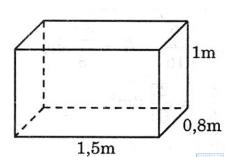
Bài 17: Tính thể tích hình sau:
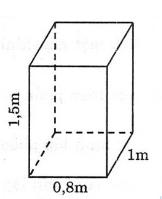
Bài 18: Tính thể tích của một hình hộp chữ nhật có diện tích xung quanh bằng 448 cm2, chiều cao 8 cm, chiều dài hơn chiều rộng 4 cm
Bài 19: Tính thể tích hình hộp chữ nhật không nắp biết chiều dài 75 cm, chiều rộng 40 cm và chiều cao 35 cm.
Bài 20: Tính thể tích hình hộp chữ nhật có chiều dài a, chiều rộng b và chiều cao c:
a) a = 7 cm; b = 5 cm; c = 12cm
b) a = 3 m; b = 2 m; c = 1 m
Bài 21: Một hình lập phương có thể tích bằng 729m3. Tính diện tích toàn phần của hình lập phương đó.
Bài 22: Một hình hộp chữ nhật có chiều dài bằng 15cm, chiều rộng 8dm và chiều cao bằng 10dm. Một hình lập phương có cạnh bằng trung bình cộng của ba kích thước trên hình hộp chữ nhật.
a) Tính thể tích hình hộp chữ nhật.
b) Tính thể tích hình lập phương.
Bài 23: Một hình lập phương và một hình hộp chữ nhật có thể tích bằng nhau. Cạnh của hình lập phương bằng chiều cao hình hộp chữ nhật. Đáy hình hộp chữ nhật có chiều dài 40cm, chiều rộng 10cm.
a) Tính diện tích xung quanh của hình hộp chữ nhật.
b) Tính thể tích của hình lập phương
Bài 24: Một hình lập phương có diện tích toàn phần là 294 cm². Hỏi hình lập phương đó có thể tích bao nhiêu?
Bài 25: Một cái bể hình lập phương cạnh 1,5m. Bể không có nước, người ta đổ vào 63 thùng nước, mỗi thùng 25 lít nước. Hỏi mực nước trong bể còn cách miệng bể bao nhiêu mét?
Bài 26: Một bể nước hình lập phương cạnh 1,5m. Bể đang chứa đến 3/5 bể. Người ta gánh nước đổ vào bể, mỗi gánh 30 lít nước. Hỏi phải đổ vào bể bao nhiêu gánh nước như thế để bể đầy? Mỗi lần gánh nước hết 15 phút, hỏi người này gánh nước trong bao lâu thì bể đầy?
Bài 27: Một cái bể hình lập phương cạnh 1,4m. Bể hiện đang đầy nước, người ta bơm hết nước từ bể này sang một bể thứ hai không có nước hình lập phương có cạnh 2m. Hỏi mực nước trong bể thứ hai còn cách miệng bể bao nhiêu mét?
Bài 28: Một cái thùng hình lập phương cạnh 1,2m. Thùng chứa đầy nước. Người ta bỏ vào thùng một khối sắt hình lập phương cạnh 0,6m thì nước trong thùng trào ra. Hỏi:
a, Số nước trong thùng trào ra là bao nhiêu lít?
b, Sau đó người ta lấy khối sắt ra thì mực nước trong thùng cao bao nhiêu?
