Toán chuyển động trên dòng nước lớp 5 và cách giải
Hamchoi.vn giới thiệu 50 bài tập Toán chuyển động trên dòng nước lớp 5 và cách giải lớp 5 gồm các dạng bài tập có phương pháp giải chi tiết và các bài tập điển hình từ cơ bản đến nâng cao giúp học sinh biết cách làm. Bên cạnh có là 8 bài tập vận dụng để học sinh ôn luyện dạng Toán 5 này.
Toán chuyển động trên dòng nước lớp 5 và cách giải
I) Lý thuyết
Nếu vật chuyển động ngược dòng thì có lực cản của dòng nước; nếu vật chuyển động xuôi dòng thì có thêm vận tốc dòng nước.
Khi thuyển chuyển động xuôi dòng nước:
- Vận tốc xuôi dòng = vận tốc thuyền khi dòng nước đứng yên + vận tốc dòng nước.
- Thời gian xuôi dòng = Độ dài quãng đường : vận tốc xuôi dòng.
Khi thuyền chuyển động ngược dòng nước:
- Vận tốc ngược dòng = vận tốc thuyền khi dòng nước đứng yên – vận tốc dòng nước.
- Thời gian xuôi dòng = Độ dài quãng đường : vận tốc ngược dòng.
II) Các dạng bài tập
Dạng 1: Tính vận tốc xuôi dòng, vận tốc ngược dòng, vận tốc thực hoặc vận tốc dòng nước
Phương pháp: Một số công thức cần nhớ:
Vận tốc của thuyền = ( vận tốc xuôi dòng + vận tốc ngược dòng) : 2
Vận tốc dòng nước = ( vận tốc xuôi dòng – vận tốc ngược dòng) : 2
Vận tốc xuôi dòng = vận tốc thuyền khi dòng nước đứng yên + vận tốc dòng nước.
Vận tốc ngược dòng = vận tốc thuyền khi dòng nước đứng yên – vận tốc dòng nước.
Ví dụ: Hai bến A và B cách nhau 40km. Một chiếc thuyền đi xuôi dòng từ bến A đến bến B hết 2 giờ. Hỏi vận tốc của chiếc thuyền khi nước yên lặng là bao nhiêu, biết rằng vận tốc của dòng nước là 2km/ giờ.
Lời giải
Vận tốc của thuyền khi đi xuôi dòng là:
40 : 2 = 20 (km/ giờ)
Vận tốc của thuyền khi nước yên lặng là:
20 – 2 = 18 (km/ giờ)
Đáp số: 18 km/ giờ
Dạng 2: Tìm thời gian khi đi xuôi dòng, ngược dòng
Phương pháp:
Thời gian xuôi dòng = Quãng đường : vận tốc xuôi dòng.
Thời gian ngược dòng = Quãng đường : vận tốc ngược dòng.
Ví dụ: Một con thuyền có vận tốc khi nước lặng là 7,5km / giờ. Vận tốc dòng nước là 2,5km/ giờ. Quãng đường sông từ A đến B dài 15km. Hỏi:
a) Thuyền đi xuôi dòng từ A đến B hết bao nhiêu thời gian?
b) Thuyền đi ngược dòng từ B đến A hết bao nhiêu thời gian?
Lời giải
a) Vận tốc của thuyền khi đi xuôi dòng là:
7,5 + 2,5 = 10 (km/giờ)
Thời gian thuyền đi xuôi dòng là:
15 : 10 = 1,5 (giờ)
b) Vận tốc của thuyền khi đi ngược dòng là:
7,5 – 2,5 = 5 (km/giờ)
Thời gian thuyền đi ngược dòng là:
15 : 5 = 3 (giờ)
Đáp số: a) 1,5 giờ
b) 3 giờ
Dạng 3: Tìm thời gian gặp nhau khi vật đi xuôi dòng, ngược dòng
Phương pháp:
B1: Tính vận tốc khi đi xuôi dòng, ngược dòng của vật
B2: Tìm thời gian hai vật gặp nhau
Ví dụ: Hai bến sông A và B cách nhau 32km. Cùng một lúc thuyền thứ nhất đi xuôi dòng từ A đến B và thuyền thứ hai đi từ B đến A. Hỏi sau bao lâu hai thuyền sẽ gặp nhau, biết rằng vận tốc của hai thuyền khi nước yên lặng bằng 16km/ giờ và vận tốc dòng nước là 2km/ giờ?
Lời giải:
Vận tốc của thuyền thứ nhất là:
16 + 2 = 18 (km)
Vận tốc của thuyền thứ hai là:
16 – 2 = 14 (km)
Sau mỗi giờ, hai thuyền đi được quãng đường là:
18 + 14 = 32 (km)
Thời gian đi để hai thuyền gặp nhau là:
32 : 32 = 1 (giờ)
Đáp số: 1 giờ
III) Bài tập vận dụng
Bài 1: Một ca nô xuôi dòng từ A đến B hết 2 giờ và ngược dòng từ B về A hết 4 giờ. Hỏi một cụm bèo trôi theo dòng nước từ A đến B hết mấy giờ?
Lời giải:
Trung bình mỗi giờ ca nô xuôi dòng được là: ( Quãng sông AB)
Trung bình mỗi giờ ca nô đi ngược dòng được là: ( Quãng sông AB)
Vì hiệu vận tốc xuôi dòng và ngược dòng bằng hai lần vận tốc dòng nước, nên mỗi giờ cụm bèo trôi được là: ( Quãng sông AB)
Thời gian cụm bèo trôi từ A đến B là: (giờ)
Đáp số: 8 giờ
Bài 2: Lúc 6 giờ sáng một chuyến tàu thuỷ chở khách xuôi dòng từ A đến B nghỉ lại 2 giờ để trả và đón khách rồi lại ngược dòng về đến A lúc 3 giờ 20 phút chiều cùng ngày. Hãy tính khoảng cách giữa hai bến A và B, biết rằng thời gian xuôi dòng nhanh hơn thời gian ngược dòng 40 phút và vận tốc của dòng nước là 50m/phút.
Lời giải:
Tổng thời gian xuôi dòng và ngược dòng (không tính thời gian nghỉ là):
15 giờ 20 phút - 6 giờ - 2 giờ = 7 giờ 20 phút
Đổi 7 giờ 20 phút = giờ; 40 phút =
giờ
Thời gian ngược dòng của tàu thủy là: (giờ)
Thời gian xuôi dòng của tàu thủy là: (giờ)
Trung bình mỗi giờ, tàu thủy ngược dòng được là (quãng đường AB)
Trung bình mỗi giờ, tàu thủy xuôi dòng được là: (quãng đường AB)
Trung bình mỗi giờ, đám bèo trôi được: (quãng đường AB)
Thời gian đám bèo trôi là: (giờ)
Đổi 40 giờ = 2400 phút
Khoảng cách giữa hai bến A và B là: 50 x 2400 = 120000 (m)
Đổi 120000m = 120km
Đáp số: 120km
Bài 3: Một nhóm các bạn bơi thuyền đi chơi xuôi dòng sông với vận tốc là 6km/giờ và bơi ngược dòng với vận tốc là 3km/giờ. Hỏi
a, Nếu chuyến đi chơi kéo dài 4 giờ thì khi rời bến bao xa thì các bạn phải quay lại để trở về đúng giờ?
b, Vận tốc của dòng sông?
c, Vận tốc thực của thuyền?
Lời giải:
a, Tỉ số vận tốc xuôi dòng và vận tốc ngược dòng là: 6 : 3 = 2
Vậy tỉ số thời gian xuôi dòng và thời gian ngược dòng là
Thời gian rời bến là: (giờ)
Các bạn đó rời bến số ki-lô-mét là: (km)
b, Vận tốc dòng nước là: (6 - 3) : 2 = 1,5 (km/giờ)
c, Vận tốc thực của thuyền là: 6 - 1,5 = 4,5 (km/giờ)
Đáp số: a, 8km; b, 1,5km/giờ; c, 4,5km/giờ
Bài 4: Một ca nô đi xuôi dòng nước với vận tốc 30,5 km/giờ và đi ngược dòng nước với vận tốc 24,5 km/giờ. Tính vận tốc của dòng nước?
Bài 5: Vận tốc của dòng nước là 1,6 km/giờ và một con thuyền đi với vận tốc 7,2 km/giờ khi nước lặng.
a) Nếu thuyền đi ngược dòng thì sau 5,5 giờ sẽ đi được bao nhiêu km?
b) Nếu thuyền đi xuôi dòng thì cần bao nhiêu thời gian để đi được quãng đường như khi ngược dòng trong 5,5 giờ?
Bài 6: Một ca nô đi xuôi dòng từ A đến B hết 32 phút và ngược dòng từ B về A hết 48 phút. Hỏi một cụm bèo trôi từ A về B hết bao lâu?
Phân tích 1
+ Trên cùng một quãng đường thì vận tốc và thời gian là hai đại lượng tỉ lệ nghịch.
+ Thời gian bèo trôi từ A đến B chính là thời gian dòng nước chảy từ A đến B
+ Vận tốc xuôi dòng – vận tốc ngược dòng
= Vận tốc ca nô + vận tốc dòng nước - vận tốc ca nô + vận tốc dòng nước
= 2 lần vận tốc dòng nước
Cách giải 1
+ Tỉ số thời gian ca nô xuôi dòng và ngược dòng là:
+ Trên cùng quãng đường AB nên vận tốc và thời gian là hai đại lượng tỉ lệ nghịch với nhau, nên ta có tỉ số giữa vận tốc xuôi dòng và ngược dòng là:
Ta có sơ đồ sau:
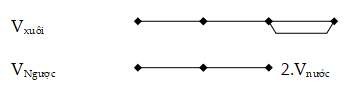
Nhìn vào sơ đồ ta có: Vxuôi = 3 x 2Vnước = 6 x Vnước
Vì trên cùng một quãng đường thời gian tỉ lệ nghịch với vận tốc
Nên thời gian cụm bèo trôi = 6 x thời gian xuôi dòng = 6 x 32phút = 192 phút
Đáp số: 192 phút
Lời giải:
Tỉ số thời gian ca nô xuôi dòng và ca nô ngược dòng là:
32 : 48 = 2/3
Tỉ số giữa vận tốc xuôi dòng và vận tốc ngược dòng của ca nô là:
1 : 2/3 = 3/2
Thời gian cụm bèo trôi là:
32 x 6 = 192 (phút)
Đáp số: 192 phút
Phân tích 2:
+ Ta đi tìm trung bình mỗi giờ ca nô đi xuôi dòng được số phần của quãng sông AB là bao nhiêu.
+ Trung bình mỗi giờ ca nô đi ngược dòng được số phần của quãng sông AB là bao nhiêu.
+ Tính trung bình mỗi giờ cụm bèo trôi được bao nhiêu phần của quãng sông AB
Lời giải:
Trung bình mỗi giờ ca nô xuôi dòng được là:
1 : 32 = 1/32 ( Quãng sông AB)
Trung bình mỗi giờ ca nô đi ngược dòng được là:
1 : 48 = 1/48 ( Quãng sông AB)
Vì hiệu vận tốc xuôi dòng và ngược dòng bằng hai lần vận tốc dòng nước, nên mỗi giờ cụm bèo trôi được là:
( Quãng sông AB)
Thời gian cụm bèo trôi từ A đến B là:
1 : 1/192 = 192 (phút)
Đáp số: 192 phút
Bài 7: Một ca nô chạy trên một khúc sông từ bến A đến bến B, khi đi xuôi dòng thì mất 5 giờ, khi đi ngược dòng thì mất 6 giờ. Tính khoảng cách từ bến A đến bến B, biết vận tốc của ca nô khi đi xuôi dòng hơn vân tốc của ca nô khi đi ngược dòng là 6km/giờ?
Phân tích 1:
+ Cần phải tính được vận tốc xuôi dòng hoặc là vận tốc ngược dòng.
+ Lấy vận tốc vừa tìm được nhân với thời gian tương ứng
+ Trên cùng một quãng đường thì vận tốc và thời gian là hai đại lượng tỉ lệ nghịch.
Cách giải 1
Tỉ số thời gian xuôi dòng và ngược dòng là:
Trên cùng một quãng sông AB thì vận tốc và thời gian là hai đại lượng tỉ lệ nghịch với nhau, nên ta có tỉ số giữa vận tốc xuôi dòng và ngược dòng là:
Ta có sơ đồ sau:

Nhìn vào sơ đồ ta có:
Vận tốc xuôi dòng là: 6 x 6 = 36 (km/giờ)
Khoảng cách bến sông AB là 36 x 5 = 180 (km)
Đáp số: 180 km
Lời giải:
Tỉ số thời gian xuôi dòng và thời gian ngược dòng là:
5 : 6 = 5/6
Tỉ số giữa vận tốc xuôi dòng và vận tốc ngược dòng là:
1 : 5/6 = 6/5
Vận tốc xuôi dòng là:
6 x 6 = 36 (km/giờ)
Khoảng cách bến sông AB là:
36 x 5 = 180 (km)
Đáp số: 180km
Phân tích 2:
+ Ta đi tìm trung bình mỗi giờ ca nô đi xuôi dòng được số phần của quãng sông AB là bao nhiêu.
+ Trung bình mỗi giờ ca nô đi ngược dòng được số phần của quãng sông AB là bao nhiêu.
+ Tính trung bình mỗi giờ dòng nước trôi được bao nhiêu phần của quãng sông AB
+ Vận tốc xuôi dòng hơn vận tốc ngược dòng 6km/giờ đó chính là 2 lần vận tốc của dòng nước, từ đó ta tính được vận tốc của dòng nước
Cách giải 2:
Trung bình mỗi giờ ca nô xuôi dòng được là:
1 : 5 = 1/5 (quãng sông)
Trung bình mỗi giờ ca nô đi ngược dòng được là:
1 : 6 = 1/6(quãng sông)
Vì hiệu vận tốc xuôi dòng và ngược dòng bằng hai lần vận tốc dòng nước nên mỗi giờ dòng nước chảy được là:
(quãng sông)
Thời gian dòng nước chảy từ A đến B là:
1 : 1/60 = 60 (giờ)
Vận tốc của dòng nước là:
6 : 2 = 3 (km/giờ)
Quãng sông AB là:
60 x 3 = 180 (km)
Đáp số: 180 km
Bài 8: Một ca nô xuôi dòng từ A đến B hết 4 giờ và ngược dòng từ B về A hết 6 giờ. Biết vận tốc của dòng nước 50m/phút. Tính
a, Chiều dài quãng sông AB
b, Vận tốc ca nô trong nước yên lặng.
Phân tích 1
+ Trên cùng một quãng đường thì vận tốc và thời gian là hai đại lượng tỉ lệ nghịch.
+ Để tính chiều dài quãng sông AB ta có thể tiến hành theo nhiều cách: Vận tốc xuôi dòng nhân với thời gian xuôi dòng hoặc vận tốc ngược dòng nhân với thời gian ngược dòng hoặc vận tốc dòng nước nhân với thời gian của dòng nước trôi từ A đến B
+ Vận tốc ca nô trong nước lặng chính là vận tốc thực của ca nô = vận tốc xuôi dòng – vận tốc của dòng nước hoặc là = vận tốc ngược dòng + vận tốc dòng nước.
Cách giải 1
Vận tốc dòng nước là: 50m/phút = 3km/giờ
Tỉ số thời gian xuôi dòng và ngược dòng là:
Trên cung một quãng đường thì vận tốc và thời gian là hai đại lượng tỉ lệ nghịch với nhau
Nên tỉ số vận tốc xuôi dòng và ngược dòng là :
Ta có sơ đồ vận tốc sau:
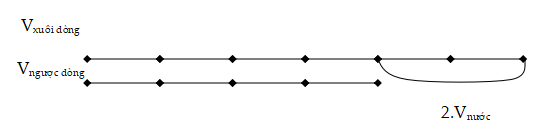
Vì trên cùng một quãng đường thì vận tốc và thời gian là hai đại lượng tỉ lệ nghịch với nhau nên thời gian dòng nước trôi từ A đến B là: 4 x 6 = 24 (giờ)
a, Quãng sông AB là: 3 x 24 = 72 (km)
b, Vận tốc của ca nô đi trong nước lặng là: (3 x 6) – 3 = 15 (km/giờ)
Đáp số: a, 72 km/ b, 15 km/giờ
Cách giải 2:
Trung bình mỗi giờ ca nô xuôi dòng được là:
1 : 4 = 1/4 (quãng sông AB)
Trung bình mỗi giờ ca nô ngược dòng được là:
1 : 6 = 1/6 (quãng sông AB)
Vì hiệu vận tốc xuôi dong và ngược dòng bằng hai lần vận tốc dòng nước, nên mỗi giờ dòng nước chảy được là: (quãng sông AB)
Thời gian dòng nước chảy từ A đến B là:
1 : 1/24 = 24 (giờ)
a, Ta có vận tốc dòng nước là: 50m/phút = 3km/giờ
Quãng sông AB dài là:
3 x 24 = 72 (km)
Vận tốc của ca nô khi đi trong nước lặng là: 72 : 6 + 3 = 15 (km/giờ)
Đáp số: a, 72 km
b, 15 km/giờ
