Giải sách bài tập Toán lớp 10 Bài 3: Khái niệm vectơ

Bài 22 trang 85 SBT Toán 10 Tập 1: Trong mặt phẳng cho hai điểm phân biệt A, B. Tập hợp tất cả các điểm M thỏa mãn $\overrightarrow{AM}$ ngược hướng với $\overrightarrow{AB}$ là hình gì?

A. Đường thẳng AB.

B. Tia AB.

C. Tia đối của tia AB trừ điểm A.

D. Đoạn thẳng AB.

Lời giải:

Đáp án đúng là C

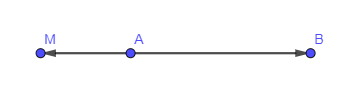
Ta có vectơ $\overrightarrow{AM}$ ngược hướng với vectơ $\overrightarrow{AB}$nên A, M, B thẳng hàng và M khác phía với B so với A.

Do đó tập hợp điểm M là tia đối của tia AB trừ đi điểm A.

Bài 23 trang 85 SBT Toán 10 Tập 1: Trong mặt phẳng cho hai điểm phân biệt A, B. Tập hợp tất cả các điểm M thỏa mãn $\left|\overrightarrow{AM}\right|=\left|\overrightarrow{AB}\right|$ là hình gì?

A. Đường trung trực của đoạn thẳng AB.

B. Đường tròn tâm A bán kính AB.

C. Đường tròn tâm B bán kính AB.

D. Đoạn thẳng AB.

Lời giải:

Đáp án đúng là B

Ta có: $\left|\overrightarrow{AM}\right|=\left|\overrightarrow{AB}\right|$ 

Điểm M là điểm thỏa mãn độ dài vectơ $\overrightarrow{AM}$ bằng độ dài vectơ $\overrightarrow{AB}$ nghĩa là điểm M cách A một khoảng không đổi bằng độ dài vectơ $\overrightarrow{AB}$ là đường tròn tâm A bán kính AB.

Bài 24 trang 85 SBT Toán 10 Tập 1: Cho hình thang ABCD có AB và CD song song với nhau. Phát biểu nào dưới đây là đúng?

A. $\overrightarrow{AB}=\overrightarrow{CD}$.

B. $\overrightarrow{AB}$ và $\overrightarrow{DC}$ cùng hướng.

C. $\overrightarrow{AB}$ và $\overrightarrow{DC}$ ngược hướng.

D. $\overrightarrow{AB}=\overrightarrow{DC}$.

Lời giải:

Đáp án đúng là B

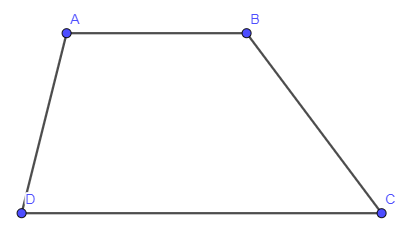
Vì ABCD là hình thang và AB // CD nên hai vectơ $\overrightarrow{AB}$ và $\overrightarrow{DC}$ cùng hướng.

Bài 25 trang 85 SBT Toán 10 Tập 1: Cho $\overrightarrow{a}=\overrightarrow{b}$. Phát biểu nào dau đây là sai?

A. $\overrightarrow{a}$ và $\overrightarrow{b}$ cùng hướng.

B. $\overrightarrow{a}$ và $\overrightarrow{b}$ cùng độ dài.

C. $\overrightarrow{a}$ và $\overrightarrow{b}$ không cùng phương.

D. $\overrightarrow{a}$ và $\overrightarrow{b}$ cùng phương.

Lời giải:

Đáp án đúng là C

Ta có $\overrightarrow{a}=\overrightarrow{b}$ thì $\overrightarrow{a}$ và $\overrightarrow{b}$ cùng hướng và cùng độ dài.

Vì $\overrightarrow{a}$ và $\overrightarrow{b}$ cùng hướng nên $\overrightarrow{a}$ và $\overrightarrow{b}$ cùng phương.

Do đó A, B, D đúng và C sai.

Bài 26 trang 85 SBT Toán 10 Tập 1: Cho điểm I là trung điểm của đoạn thẳng AB. Phát biểu nào sau đây là đúng?

A. $\overrightarrow{IA}=\overrightarrow{IB}$.

B. $\overrightarrow{IA}$ và $\overrightarrow{IB}$ cùng hướng.

C. $\overrightarrow{AI}=\overrightarrow{BI}$.

D. $\overrightarrow{AI}=\overrightarrow{IB}$

Lời giải:

Đáp án đúng là D

I là trung điểm của AB nên IA = IB.

Hơn nữa ta thấy vectơ $\overrightarrow{IA}$ và vectơ $\overrightarrow{IB}$ cùng phương và ngược hướng nên $\overrightarrow{IA}=-\overrightarrow{IB}$ hay $\overrightarrow{AI}=\overrightarrow{IB}$.

Bài 27 trang 85 SBT Toán 10 Tập 1: Cho năm điểm A, B, C, D, E.

a) Viết các vectơ khác $\overrightarrow{0}$ có cùng điểm đầu là A, điểm cuối là một trong các điểm đã cho.

b) Viết các vectơ khác $\overrightarrow{0}$ có cùng điểm cuối là B, điểm đầu là một trong các điểm đã cho.

Lời giải:

a) Các vectơ khác $\overrightarrow{0}$ có cùng điểm đầu là A, điểm cuối là một trong các điểm đã cho là: $\overrightarrow{\text{AA}},\overrightarrow{AB},\overrightarrow{AC},\overrightarrow{AD},\overrightarrow{AE}$.

b) Các vectơ khác $\overrightarrow{0}$ có cùng điểm cuối là B, điểm đầu là một trong các điểm đã cho là: $\overrightarrow{AB},\overrightarrow{BB},\overrightarrow{CB},\overrightarrow{DB},\overrightarrow{EB}$.

Bài 28 trang 85 SBT Toán 10 Tập 1: Cho hình vuông ABCD có cạnh bằng a. Tính $\left|\overrightarrow{AB}\right|,\left|\overrightarrow{AC}\right|$.

Lời giải:

Vì ABCD là hình vuông cạnh a nên $\left|\overrightarrow{AB}\right|=a$.

Xét tam giác ABC vuông tại B, có:

AC² = AB² + BC²

⇔ AC² = a² + a²

⇔ AC² = 2a²

⇔ AC = $\sqrt{2}$a.

⇒ $\left|\overrightarrow{AC}\right|=\sqrt{2}a$.

Vậy $\left|\overrightarrow{AB}\right|=a$ và  $\left|\overrightarrow{AC}\right|=\sqrt{2}a$.

Bài 29 trang 85 SBT Toán 10 Tập 1: Cho tam giác ABC. Gọi M, N, P lần lượt là trung điểm BC, CA, AB. Chứng minh rằng:

a) $\overrightarrow{MN}=\overrightarrow{PA}$.

b) $\overrightarrow{MP}=\overrightarrow{CN}$.

Lời giải:

a) Xét tam giác ABC, có:

M là trung điểm của BC

N là trung điểm của AC

⇒ MN là đường trung bình của tam giác ABC

⇒ MN // BC và MN = $\frac{1}{2}$BC

Mà PA = PB = $\frac{1}{2}$BC

⇒ PA = MN

Vì MN // BC nên hai vectơ $\overrightarrow{MN}$ và $\overrightarrow{PA}$ cùng phương, cùng hướng và PA = MN. Do đó $\overrightarrow{MN}=\overrightarrow{PA}$.

b) Xét tam giác ABC, có:

M là trung điểm của BC

P là trung điểm của AB

⇒ MP là đường trung bình của tam giác ABC

⇒ MP // AC và MP = $\frac{1}{2}$AC

Mà CN = AN = $\frac{1}{2}$AC

⇒ MP = CN

Vì MP // AC nên hai vectơ $\overrightarrow{MP}$ và $\overrightarrow{AC}$ cùng phương, cùng hướng và MP = CN. Do đó $\overrightarrow{MP}=\overrightarrow{CN}$.

Bài 30 trang 86 SBT Toán 10 Tập 1: Trong mặt phẳng nghiêng không có ma sát cho hệ vật m₁, m₂, hai vật nối với nhau bằng một sợi dây không dãn vắt qua ròng rọc (Hình 32). Giả sử bỏ qua khối lượng của dây và ma sát của ròng rọc.

a) Tìm các cặp vec tơ cùng phương trong các cặp vectơ ở Hình 32.

b) Những cặp vectơ cùng phương đó có cùng hướng không?

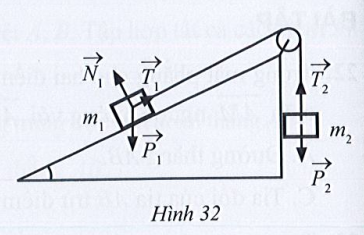
Lời giải:

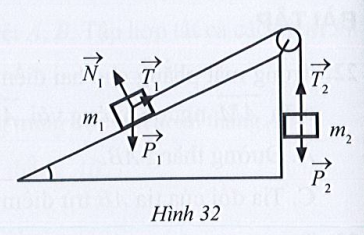
Các cặp vectơ cùng phương là: 

Bài 31* trang 86 SBT Toán 10 Tập 1: Cho đường tròn tâm O và dây cung BC không đi qua O. Điểm A chuyển động trên cung lớn BC của đường tròn sao cho tam giác ABC nhọn. Gọi H là trực tâm của tam giác ABC. Chứng minh rằng $\overrightarrow{AH}$ có độ dài không đổi.

Lời giải:

Kẻ đường kính AK (K ∈ (O)), gọi M là trung điểm của BC.

Vì H là trực tâm nên BH ⊥ AC, KC ⊥ AC ($\widehat{ACK}$ là góc nội tiếp chắn nửa đường tròn)

⇒ BH // KC

Chứng minh tương tự ta được CH // BK (cùng ⊥ AB)

⇒ BHCK là hình bình hành

Ta có M là trung điểm BC nên M là trung điểm của HK

Xét tam giác AHK, có:

O là trung điểm AC

M là trung điểm HK

⇒ OM là đường trung bình của tam giác AHK

⇒ OM // AH và $OM=\frac{1}{2}AH$

Vì O và M cố định nên OM cố định đó đó AH không đổi.