Tam thức nào sau đây luôn dương với mọi giá trị của x?
A. f(x) = x2 – 10x + 2;
B. f(x) = x2 – 2x + 1;
C. f(x) = x2 – 2x + 10;
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: C
Tam thức f(x) luôn dương với mọi giá trị của x khi và chỉ khi a > 0 và ∆ < 0.
⦁ Xét phương án A: f(x) = x2 – 10x + 2.
Ta có a = 1 > 0 và ∆ = (–10)2 – 4.1.2 = 92 > 0.
Do đó ta loại phương án A.
⦁ Xét phương án B: f(x) = x2 – 2x + 1.
Ta có a = 1 > 0 và ∆ = (–2)2 – 4.1.1 = 0.
Do đó ta loại phương án B.
⦁ Xét phương án C: f(x) = x2 – 2x + 10.
Ta có a = 1 > 0 và ∆ = (–2)2 – 4.1.10 = –36 < 0.
Do đó ta nhận phương án C.
⦁ Xét phương án D: f(x) = –x2 + 2x + 10.
Ta có a = –1 < 0.
Do đó ta loại phương án D.
Vậy ta chọn phương án C.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho tam thức bậc hai f(x) = –2x2 + 8x – 8. Trong các mệnh đề sau, mệnh đề nào đúng?
Cho hàm số y = f(x) có đồ thị như hình bên.
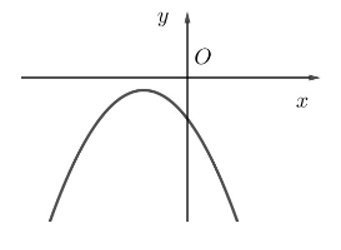
Bảng xét dấu của tam thức bậc hai tương ứng là:
Cho tam thức bậc hai f(x) = x2 + 1. Mệnh đề nào sau đây đúng nhất?
Cho tam thức bậc hai f(x) = x2 – 8x + 16. Khẳng định nào sau đây đúng?
Cho hàm số y = f(x) = ax2 + bx + c có đồ thị như hình vẽ.
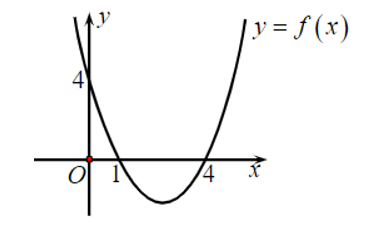
Đặt ∆ = b2 – 4ac. Chọn khẳng định đúng?
Cho tam thức bậc hai f(x) = x2 – 10x + 2. Kết luận nào sau đây đúng?
Bài 1: Dấu của tam thức bậc hai
