Trắc nghiệm Toán 10 Hàm số có đáp án (Nhận biết)
-
3641 lượt thi
-
15 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Điểm nào sau đây thuộc đồ thị hàm số y = 2 |x − 1| + 3 |x| − 2?
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: A
Đặt y = f(x) = 2 |x − 1| + 3 |x| − 2
Ta có: f(2) = 2 |2 − 1| + 3 |2| − 2 = 6 nên (2; 6) thuộc đồ thị hàm số.
Câu 2:
Điểm nào sau đây không thuộc đồ thị hàm số
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: C
Xét đáp án A, thay x = 2 và y = 0 vào hàm số ta được thỏa mãn.
Xét đáp án B, thay x = 3 và y = vào hàm số ta được thỏa mãn
Xét đáp án C, thay x = 1 và y = -1 vào hàm số ta được không thoả mãn
Câu 3:
Cho hàm số . Tính f(4), ta được kết quả:
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: B
Ta thấy x = 4 ∈ (2; 5] ⇒ f(4) =42 – 1 = 15.
Câu 4:
Cho hàm số y = f (x) = |−5x|. Khẳng định nào sau đây là sai?
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: D
Ta có · f(−1) = |−5.(−1)| = |5| = 5⇒ A đúng.
f(2) = |−5.2| = |−10| = 10 ⇒ B đúng.
f(−2) = |−5.(−2)| = |10| = 10 ⇒ C đúng.
f ⇒ D sai.
Câu 5:
Tập xác định của hàm số là
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: B
Vậy tập xác định của hàm số là: R
Câu 6:
Tìm tập xác định D của hàm số
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: B
Hàm số xác định khi
Vậy tập xác định của hàm số là:
Câu 7:
Cho hai hàm số f(x) và g(x) cùng đồng biến trên khoảng (a; b). Có thể kết luận gì về chiều biến thiên của hàm số y = f(x) + g(x) trên khoảng (a; b)?
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: A
Vì f(x) và g(x) cùng đồng biến trên khoảng (a; b) nên với x1, x2 ∈ (a; b) mà
x1 < x2 thì:⇒ f(x1) + g(x1) < f(x2) + g(x2)
Do đó y = f(x) + g(x) cũng đồng biến trên (a; b).
Câu 8:
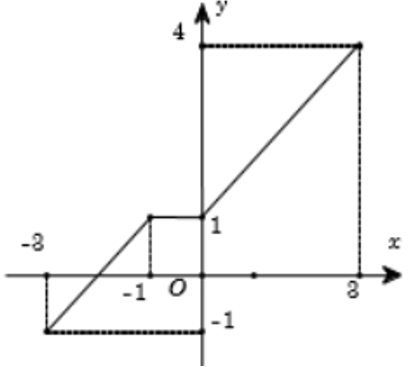
Cho hàm số y = f(x) có tập xác định là [−3; 3] và đồ thị của nó được biểu diễn bởi hình bên. Khẳng định nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: A
Trên khoảng (−3; −1) và (1; 3) đồ thị hàm số đi lên từ trái sang phải
⇒ Hàm số đồng biến trên khoảng (−3; −1) và (1; 3).
Câu 9:
Tìm tập xác định D của hàm số
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: C
Hàm số xác định khi x2 – 16 > 0 ⇔ x2 > 16 ⇔
Vậy tập xác định của hàm số là D = (−∞; −4) ∪ (4; +∞).
Câu 11:
Cho hàm số: y = f(x) = |2x − 3|. Tìm x để f(x) = 3.
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: B
Ta có: f(x) = |2x − 3| = 3 ⇔
Vậy x = 3 hoặc x = 0.
Câu 12:
Câu nào sau đây đúng?
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: C
+) Hàm số y = a2x + b đồng biến khi a2 > 0 ⇔ a ≠ 0 nên A, B và D sai.
+) Hàm số y = -a2x + b nghịch biến khi –a2 < 0 ⇔ a ≠ 0 nên C đúng.
Câu 13:
Xét tính chất chẵn lẻ của hàm số y = 2x3 + 3x + 1. Trong các mệnh đề sau, tìm mệnh đề đúng?
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: C
TXĐ: R.
Ta có: f(−x) = 2.(−x)3 + 3.(−x) + 1 = −2x3 − 3x + 1
Do đó y = f(x) là hàm số không chẵn cũng không lẻ.
Câu 14:
Xét tính chẵn, lẻ của hai hàm số f(x) = |x + 2| − |x − 2|, g(x) = −|x|
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: B
Các hàm số y = f(x), y = g(x) đều xác định trên R và có –x ∈ R
Ta có:
f(−x) = |−x + 2| − |−x − 2| = |x − 2| − |x + 2| = −f(x) nên y = f(x) là hàm số lẻ.
g(−x) = −|−x| = −|x| = g(x) nên y = g(x) là hàm số chẵn.
Câu 15:
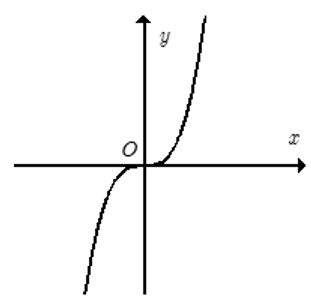
Cho đồ thị hàm số y = x3 như hình bên. Khẳng định nào sau đây sai?
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: D
Quan sát đồ thị hàm số ta thấy, hàm số đồng biến trên R nên các đáp án A, B, C đều đúng.
Đáp án D sai vì không có khái niệm hàm số đồng biến tại một điểm.
