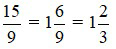Sắp xếp các khối lượng sau theo thứ tự từ lớn đến nhỏ:
\[3\frac{3}{4}\] tạ; \[\frac{{377}}{{100}}\] tạ; \[\frac{7}{2}\] tạ; \[3\frac{{45}}{{100}}\] tạ; 365 kg
Giải bởi Vietjack
Trả lời:
Ta có:
\[3\frac{3}{4}\] tạ = \[\frac{{15}}{4}\] tạ = \[\frac{{377}}{{100}}\] tạ
\[\frac{7}{2}\] tạ = \[\frac{{350}}{{100}}\] tạ
\[3\frac{{45}}{{100}}\] tạ = \[\frac{{365}}{{100}}\] tạ
→ Các khối lượng theo thứ tự từ lớn đến nhỏ là:
\[\frac{{377}}{{100}}\] tạ; \[3\frac{3}{4}\] tạ; ; 365 kg; \[\frac{7}{2}\] tạ; \[3\frac{{45}}{{100}}\] tạ
Đáp án cần chọn là: C
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Hai xe ô tô cùng đi được quãng đường 100 km, xe taxi chạy trong 115115 giờ và xe tải chạy trong 70 phút. So sánh vận tốc hai xe.
Giá trị của \[N = - \frac{1}{7}\left( {9\frac{1}{2} - 8,75} \right):\frac{2}{7} + 0,625:1\frac{2}{3}\] là:
Giá trị nào dưới đây của x thỏa mãn \[x - 3\frac{1}{2}x = - \frac{{20}}{7}\]
Sắp xếp theo thứ tự tăng dần 23%; \[\frac{{12}}{{100}}; - 1\frac{1}{{12}}; - \frac{{31}}{{24}};5\frac{1}{2}\]ta được
Kết quả của phép tính \[\left( { - 1\frac{1}{3}} \right) + 2\frac{1}{2}\] bằng:
Tính hợp lí \[A = \left( {4\frac{5}{{17}} - 3\frac{4}{5} + 8\frac{{15}}{{29}}} \right) - \left( {3\frac{5}{{17}} - 6\frac{{14}}{{29}}} \right)\] ta được
Tìm x biết \[\frac{{\left( {1,16 - x} \right).5,25}}{{\left( {10\frac{5}{9} - 7\frac{1}{4}} \right).2\frac{2}{{17}}}} = 75\% \]
Dùng phân số hoặc hỗn số (nếu có thể) để viết các đại lượng diện tích dưới đây theo mét vuông, ta được:
a) 125 dm2; b) 218 cm2; c) 240 dm2; d) 34 cm2
1. Quy đồng mẫu nhiều phân số
Để quy đồng hai hay nhiều phân số ta làm như sau:
Bước 1: Tìm một bội chung (thường là BCNN) của các mẫu để làm mẫu chung.
Bước 2: Tìm thừa số phụ của mỗi mẫu bằng cách chia mẫu chung cho từng mẫu.
Bước 3: Nhân tử và mẫu của mỗi phân số với thừa số phụ tương ứng.
Ví dụ 1: Để quy đồng ba phân số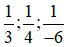 
ta làm như sau:
+ Đưa về các phân số có mẫu dương: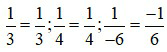 
.
+ Tìm mẫu chung: BCNN (3; 4; 6) = 12
+ Thừa số phụ:
12 : 3 = 4
12 : 4 = 3
12 : 6 = 2
Ta có:
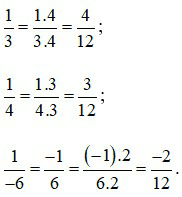
2. So sánh hai phân số
a) So sánh hai phân số cùng mẫu
– Trong hai phân số cùng một mẫu dương, phân số nào có tử lớn hơn thì phân số đó lớn hơn.
Ví dụ 2: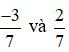 
là hai phân số có cùng mẫu số dương.
Vì –3 < 2 nên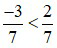 
.
b) So sánh hai phân số không cùng mẫu
– Muốn so sánh hai phân số không cùng mẫu, ta viết chúng dưới dạng hai phân số có cùng một mẫu dương rồi so sánh các tử số với nhau: phân số nào có tử số lớn hơn thì phân số đó lớn hơn.
Ví dụ 3: So sánh hai phân số sau: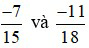 
.
BCNN (15; 18) = 90
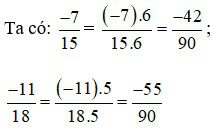
Vì –42 > –55 nên 
do đó,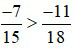
3. Hỗn số dương
– Khái niệm hỗn số dương: Với a, b, c là những số nguyên dương, ta gọi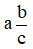 
là một hỗn số dương với a là phần nguyên và 
là phần phân số.
Ví dụ 4:
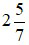là một hỗn số dương với phần nguyên là 2 và phần phân số là 
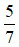. Khi đó ta đọc 
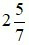là hai năm phần bảy.
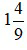là một hỗn số dương với phần nguyên là 1 và phần phân số là 
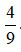. Khi đó ta đọc
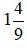là một bốn phần chín.
– Muốn đổi từ hỗn số sang phân số ta làm như sau:
Bước 1: Giữ nguyên phần mẫu số.
Bước 2: Phần tử số mới sẽ bằng phần mẫu số nhân với phần nguyên và cộng với phần tử số ban đầu.
Ví dụ 5: Đổi hỗn số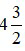 
sang phân số:
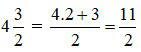
– Muốn đổi từ phân số sang hỗn số (điều kiện tử số của phân số phải lớn hơn mẫu số) ta làm như sau:
Bước 1: Giữ nguyên phần mẫu số và mẫu số này sẽ là mẫu số trong phần hỗn số mới.
Bước 2: Lấy phần tử số chia cho mẫu số, phần thương sẽ là phần nguyên trong hỗn số mới và phần dư là tử số mới của hỗn số.
Ví dụ 6: Đổi phân số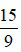 
sang hỗn số
Ta có 15 chia 9 được thương là 1 và dư 6 do đó:
