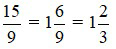Hai xe ô tô cùng đi được quãng đường 100 km, xe taxi chạy trong 115115 giờ và xe tải chạy trong 70 phút. So sánh vận tốc hai xe.
Giải bởi Vietjack
Trả lời:
Đổi 70 phút = \[\frac{7}{6}\] giờ
Vận tốc của xe taxi là:
\[100:1\frac{1}{5} = 100:\frac{6}{5} = \frac{{250}}{3} = 83\frac{1}{3}\left( {km/h} \right)\]
Vận tốc của xe tải là:
\[100:\frac{7}{5} = \frac{{600}}{7} = 85\frac{5}{7}\left( {km/h} \right)\]
Ta có: \[85\frac{5}{7} > 83\frac{1}{3}\] nên vận tốc của xe taxi lớn hơn vận tốc xe tải
Đáp án cần chọn là: B
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Sắp xếp các khối lượng sau theo thứ tự từ lớn đến nhỏ:
\[3\frac{3}{4}\] tạ; \[\frac{{377}}{{100}}\] tạ; \[\frac{7}{2}\] tạ; \[3\frac{{45}}{{100}}\] tạ; 365 kg
Giá trị của \[N = - \frac{1}{7}\left( {9\frac{1}{2} - 8,75} \right):\frac{2}{7} + 0,625:1\frac{2}{3}\] là:
Giá trị nào dưới đây của x thỏa mãn \[x - 3\frac{1}{2}x = - \frac{{20}}{7}\]
Sắp xếp theo thứ tự tăng dần 23%; \[\frac{{12}}{{100}}; - 1\frac{1}{{12}}; - \frac{{31}}{{24}};5\frac{1}{2}\]ta được
Kết quả của phép tính \[\left( { - 1\frac{1}{3}} \right) + 2\frac{1}{2}\] bằng:
Tính hợp lí \[A = \left( {4\frac{5}{{17}} - 3\frac{4}{5} + 8\frac{{15}}{{29}}} \right) - \left( {3\frac{5}{{17}} - 6\frac{{14}}{{29}}} \right)\] ta được
Tìm x biết \[\frac{{\left( {1,16 - x} \right).5,25}}{{\left( {10\frac{5}{9} - 7\frac{1}{4}} \right).2\frac{2}{{17}}}} = 75\% \]
Dùng phân số hoặc hỗn số (nếu có thể) để viết các đại lượng diện tích dưới đây theo mét vuông, ta được:
a) 125 dm2; b) 218 cm2; c) 240 dm2; d) 34 cm2
1. Quy đồng mẫu nhiều phân số
Để quy đồng hai hay nhiều phân số ta làm như sau:
Bước 1: Tìm một bội chung (thường là BCNN) của các mẫu để làm mẫu chung.
Bước 2: Tìm thừa số phụ của mỗi mẫu bằng cách chia mẫu chung cho từng mẫu.
Bước 3: Nhân tử và mẫu của mỗi phân số với thừa số phụ tương ứng.
Ví dụ 1: Để quy đồng ba phân số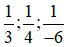 
ta làm như sau:
+ Đưa về các phân số có mẫu dương: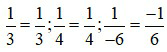 
.
+ Tìm mẫu chung: BCNN (3; 4; 6) = 12
+ Thừa số phụ:
12 : 3 = 4
12 : 4 = 3
12 : 6 = 2
Ta có:
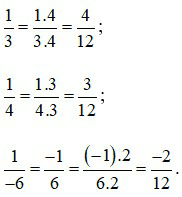
2. So sánh hai phân số
a) So sánh hai phân số cùng mẫu
– Trong hai phân số cùng một mẫu dương, phân số nào có tử lớn hơn thì phân số đó lớn hơn.
Ví dụ 2: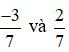 
là hai phân số có cùng mẫu số dương.
Vì –3 < 2 nên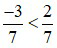 
.
b) So sánh hai phân số không cùng mẫu
– Muốn so sánh hai phân số không cùng mẫu, ta viết chúng dưới dạng hai phân số có cùng một mẫu dương rồi so sánh các tử số với nhau: phân số nào có tử số lớn hơn thì phân số đó lớn hơn.
Ví dụ 3: So sánh hai phân số sau: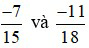 
.
BCNN (15; 18) = 90
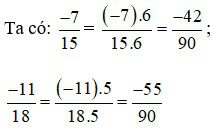
Vì –42 > –55 nên 
do đó,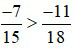
3. Hỗn số dương
– Khái niệm hỗn số dương: Với a, b, c là những số nguyên dương, ta gọi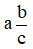 
là một hỗn số dương với a là phần nguyên và 
là phần phân số.
Ví dụ 4:
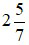là một hỗn số dương với phần nguyên là 2 và phần phân số là 
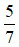. Khi đó ta đọc 
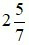là hai năm phần bảy.
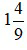là một hỗn số dương với phần nguyên là 1 và phần phân số là 
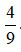. Khi đó ta đọc
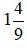là một bốn phần chín.
– Muốn đổi từ hỗn số sang phân số ta làm như sau:
Bước 1: Giữ nguyên phần mẫu số.
Bước 2: Phần tử số mới sẽ bằng phần mẫu số nhân với phần nguyên và cộng với phần tử số ban đầu.
Ví dụ 5: Đổi hỗn số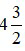 
sang phân số:
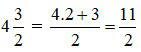
– Muốn đổi từ phân số sang hỗn số (điều kiện tử số của phân số phải lớn hơn mẫu số) ta làm như sau:
Bước 1: Giữ nguyên phần mẫu số và mẫu số này sẽ là mẫu số trong phần hỗn số mới.
Bước 2: Lấy phần tử số chia cho mẫu số, phần thương sẽ là phần nguyên trong hỗn số mới và phần dư là tử số mới của hỗn số.
Ví dụ 6: Đổi phân số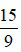 
sang hỗn số
Ta có 15 chia 9 được thương là 1 và dư 6 do đó:
