Giải bởi Vietjack
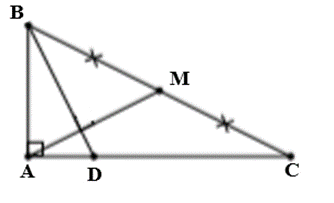
Xét tam giác ABC vuông tại A
Có: AB⊥AC ⇔ \(\overrightarrow {AB} .\overrightarrow {AC} = 0\) ⇔ \(\overrightarrow {AB} .\overrightarrow {AD} = 0\) vì D thuộc AC
Vì M là trung điểm của BC nên ta có: \(\overrightarrow {AB} + \overrightarrow {AC} = 2\overrightarrow {AM} \)
Lại có: \(\overrightarrow {BD} = \overrightarrow {AD} - \overrightarrow {AB} \) (quy tắc ba điểm)
Khi đó ta có \(2\overrightarrow {AM} .\overrightarrow {BD} \)\( = \left( {\overrightarrow {AB} + \overrightarrow {AC} } \right)\left( {\overrightarrow {AD} - \overrightarrow {AB} } \right)\)
\( = \overrightarrow {AB} .\overrightarrow {AD} - {\overrightarrow {AB} ^2} + \overrightarrow {AC} .\overrightarrow {AD} - \overrightarrow {AC} .\overrightarrow {AB} \)
\( = 0 - A{B^2} + AC.AD.cos0^\circ - 0\)
\( = - {a^2} + 2a.\frac{a}{2} = 0\).
Vậy \(\overrightarrow {AM} .\overrightarrow {BD} = 0 \Leftrightarrow \overrightarrow {AM} \bot \overrightarrow {BD} \Leftrightarrow AM \bot BD\) (đcpcm).
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Hãy viết số quy tròn của số gần đúng a = 15,318 biết \(\overline a \) = 15,318 ± 0,05.
Cho tam giác ABC vuông tại A có: AB = 4, BC = 8. Tính \(\left( {\overrightarrow {CB} ,\overrightarrow {CA} } \right)\).
Cho mẫu số liệu sau đây:
2; 5; 1; 2; 8; 5; 45; 3.
Tìm giá trị ngoại lệ của mẫu số liệu trên?
Cho β là góc tù. Tìm khẳng định đúng trong các khẳng định dưới đây?
Cho mẫu số liệu sau:
24; 16; 12; 5; 9; 3.
Tìm độ lệch chuẩn của mẫu số liệu trên (làm tròn đến hàng phần trăm).
Cho giá trị gần đúng của \(\frac{6}{{17}}\) là 0,35. Sai số tuyệt đối của số gần đúng 0,35 là:
Cho tứ giác ABCD. Gọi E, F lần lượt là trung điểm của AB, CD, O là trung điểm của EF. Khẳng định nào sau đây là đúng ?
Cho mẫu số liệu sau:
12; 2; 6; 13; 9; 21.
Tìm phương sai của mẫu số liệu trên (làm tròn đến hàng phần trăm).
Cho hình thang ABCD với hai đáy là AB, CD có: \(\left( {\overrightarrow {AB} - \overrightarrow {AD} } \right).\overrightarrow {AC} = 0\). Khẳng định nào sau đây là đúng ?
Để làm đường điện dây cao thế ở Hà Giang từ vị trí bản A đến bản B, người ta phải tránh một ngọn núi nên người ta phải nối thẳng đường dây từ bản A đến bản C dài 12 km rồi nối từ bản C đến bản B dài 8 km. Qua đo đạc người ta xác định được \(\widehat {ABC} = 65^\circ \). Hỏi so với việc nối thẳng từ bản A đến bản B, người ta tốn thêm bao nhiêu tiền, biết mỗi km dây có giá 150 000 đồng.
Cho mẫu số liệu sau:
15; 26; 5; 2; 9; 5; 28; 30; 2; 26.
Tính khoảng biến thiên của mẫu số liệu trên.
Trong mặt phẳng tọa độ, cho \(\overrightarrow u = 3\overrightarrow i - 5\overrightarrow j \). Khi đó tọa độ của vectơ \(\overrightarrow u \) là
Cho hình bình hành ABCD với giao điểm hai đường chéo là I. Khi đó:
Góc giữa vectơ \(\overrightarrow a = \left( {1; - 1} \right)\) và vectơ \(\overrightarrow b = \left( { - 2;0} \right)\) có số đo bằng:
