Cho hai điểm A(–2; 1), B(3; 5) và đường thẳng d: \(\left\{ \begin{array}{l}x = - 5 + 2t\\y = 9 - 5t\end{array} \right.\). Tọa độ của điểm H ∈ d thỏa mãn \(\left| {\overrightarrow {HA} - 2\overrightarrow {HB} } \right|\) đạt giá trị nhỏ nhất là:
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: A
Ta có H ∈ d. Suy ra H(–5 + 2t; 9 – 5t).
Ta có:
⦁ \(\overrightarrow {HA} = \left( { - 2t + 3;5t - 8} \right)\);
⦁ \(\overrightarrow {HB} = \left( { - 2t + 8;5t - 4} \right)\). Suy ra \(2\overrightarrow {HB} = \left( { - 4t + 16;10t - 8} \right)\).
Suy ra \(\overrightarrow {HA} - 2\overrightarrow {HB} = \left( {2t - 13; - 5t} \right)\).
Ta có \(\left| {\overrightarrow {HA} - 2\overrightarrow {HB} } \right| = \sqrt {{{\left( {2t - 13} \right)}^2} + {{\left( { - 5t} \right)}^2}} = \sqrt {29{t^2} - 52t + 169} \)
\( = \sqrt {29\left[ {{{\left( {t - \frac{{26}}{{29}}} \right)}^2} + \frac{{4225}}{{841}}} \right]} \)
Ta có \({\left( {t - \frac{{26}}{{29}}} \right)^2} \ge 0,\,\,\forall t \in \mathbb{R}\)
\( \Leftrightarrow {\left( {t - \frac{{26}}{{29}}} \right)^2} + \frac{{4225}}{{841}} \ge \frac{{4225}}{{841}},\,\,\forall t \in \mathbb{R}\)
\( \Leftrightarrow 29\left[ {{{\left( {t - \frac{{26}}{{29}}} \right)}^2} + \frac{{4225}}{{841}}} \right] \ge 29.\frac{{4225}}{{841}} = \frac{{4225}}{{29}},\,\,\forall t \in \mathbb{R}\)
\[ \Leftrightarrow \sqrt {29\left[ {{{\left( {t - \frac{{26}}{{29}}} \right)}^2} + \frac{{4225}}{{841}}} \right]} \ge \sqrt {\frac{{4225}}{{29}}} = \frac{{65\sqrt {29} }}{{29}},\,\,\forall t \in \mathbb{R}\].
Dấu “=” xảy ra \( \Leftrightarrow t = \frac{{26}}{{29}}\).
Với \(t = \frac{{26}}{{29}}\), ta có \(H\left( { - \frac{{93}}{{29}};\frac{{131}}{{29}}} \right)\).
Khi đó \(\left| {\overrightarrow {HA} - 2\overrightarrow {HB} } \right|\) đạt giá trị nhỏ nhất bằng \[\frac{{65\sqrt {29} }}{{29}}\] khi \(H\left( { - \frac{{93}}{{29}};\frac{{131}}{{29}}} \right)\).
Vậy ta chọn phương án A.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho điểm M nằm trên ∆: x + y – 1 = 0 và cách N(–1; 3) một khoảng bằng 5. Khi đó tọa độ điểm M là:
Đường thẳng d trong hình bên biểu thị tổng lít nước được bơm vào một bể nước theo thời gian (đơn vị: giờ).
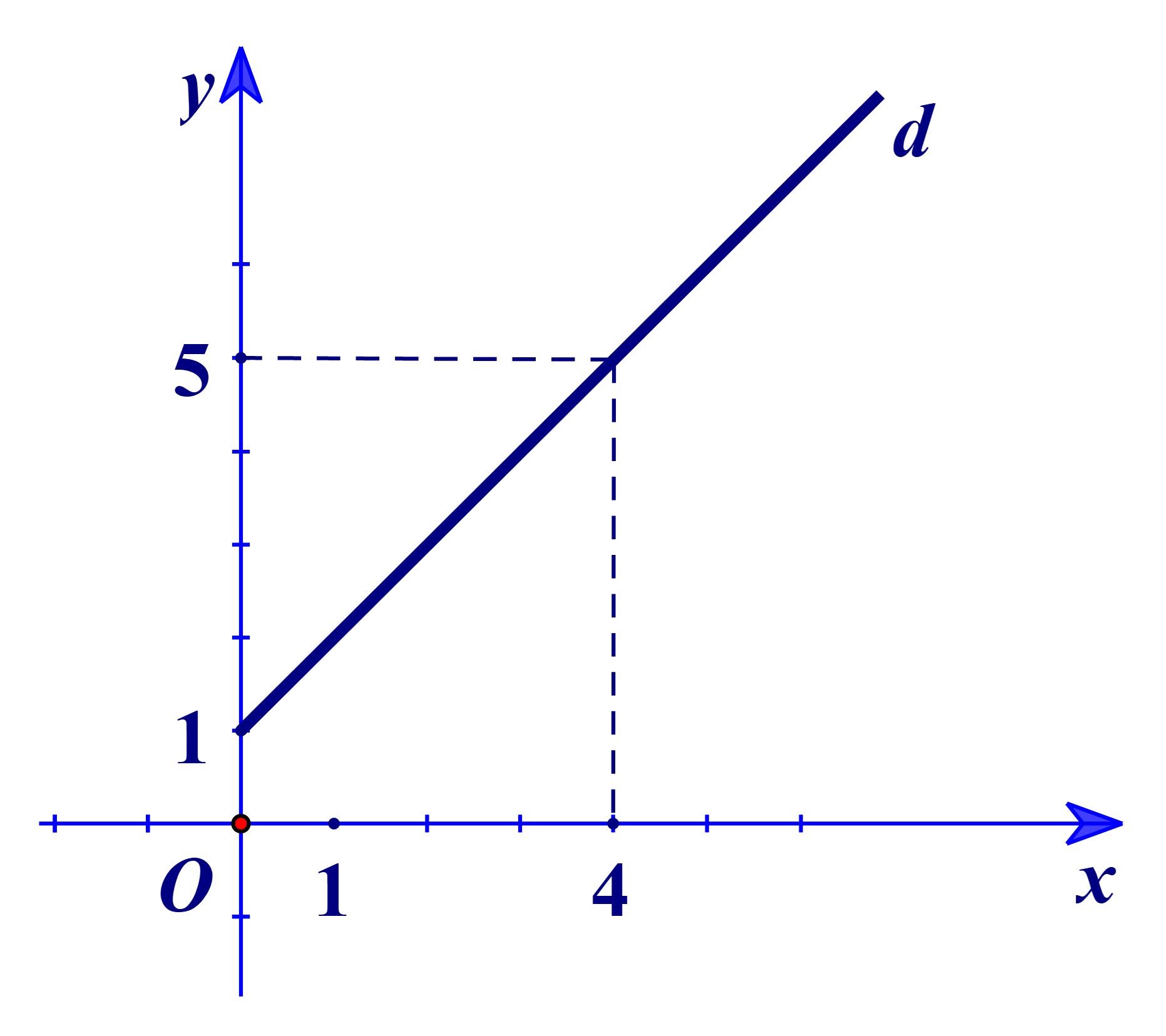
Tổng lít nước mà bể đó chứa sau 15 giờ bằng:
Bài 3. Phương trình đường thẳng