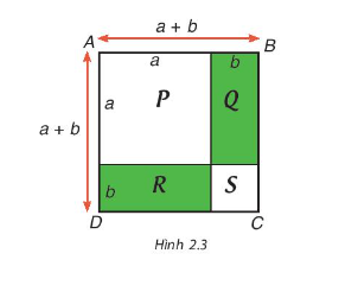
Sử dụng Hình 2.3, bằng cách tính diện tích hình vuông ABCD theo hai cách, hãy giải thích hằng đẳng thức (a + b)² = a² + 2ab + b²

Một chiếc khăn trải bàn có dạng hình chữ nhật ABCD được thêu một hoạ tiết có dạng hình thoi MNPQ ở giữa với MP = x (cm), NQ = y (cm) (x > y > 0) như Hình 5.

Viết đa thức biểu thị diện tích phần còn lại của chiếc khăn trải bàn đó.

Phân tích mỗi đa thức sau thành nhân tử:

a) \(3{x^2} - \sqrt 3 x + \frac{1}{4}\);

b) x² – x – y² + y;

c) x³ + 2x² + x – 16xy².

Tính giá trị của mỗi biểu thức sau:

a) A = 16x² ‒ 8xy + y² ‒ 21 biết 4x = y + 1;

b) B = 25x² + 60xy + 36y² + 22 biết 6y = 2 ‒ 5x;

c) C = 27x³ – 27x²y + 9xy² – y³ – 121 biết 3x = 7 + y.

Thực hiện phép tính:

a) \(7{x^2}{y^5} - \frac{7}{3}{y^2}\left( {3{x^2}{y^3} + 1} \right)\);

b) \(\frac{1}{2}x\left( {{x^2} + {y^2}} \right) - \frac{3}{2}{y^2}\left( {x + 1} \right) - \frac{1}{{\sqrt 4 }}{x^3}\);

c) (x + y)(x2 + y2 + 3xy) ‒ x3 ‒ y3;

d) (‒132xn + 1y10zn + 2 + 143xn + 2y12zn) : (11xny9zn) với n là số tự nhiên.

Cho hai đa thức: M = 23x²³y ‒ 22xy²³ + 21y ‒ 1 và N = ‒22xy³ ‒ 42y ‒ 1.

a) Tính giá trị của mỗi đa thức M, N tại x = 0; y = –2.

b) Tính M + N; M – N.

c) Tìm đa thức P sao cho M – N – P = 63y + 1.

Thực hiện phép tính:

a) \({x^3}\left( { - \frac{5}{4}{x^2}y} \right)\left( {\frac{2}{5}{x^3}{y^4}} \right)\);

b) \(\left( { - \frac{3}{4}{x^5}{y^4}} \right)\left( {x{y^2}} \right)\left( { - \frac{8}{9}{x^2}{y^5}} \right)\).