b) Tính khoảng cách từ giao điểm đó đến điểm C.
 Giải bởi Vietjack
Giải bởi Vietjack
b) Gọi E là giao điểm của tia phân giác góc A với cạnh BC.
Khoảng cách từ giao điểm đó đến điểm C tức là khoảng cách từ điểm E đến C, chính là độ dài đoạn EC.
Vì AE là tia phân giác của nên .
Vì AD // BC (vì tứ giác ABCD là hình bình hành) nên .
Do đó .
Tam giác ABE cân tại B (vì ) suy ra AB = BE.
Mà AD = BC (vì ABCD là hình bình hành).
Ta có BC = BE + EC.
Suy ra EC = BC – EC = 5 – 3 = 2 (cm).
Vậy EC = 2 cm.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho hình bình hành ABCD có AB = 3 cm, AD = 5 cm.
a) Hỏi tia phân giác của góc A cắt cạnh CD hay cạnh BC?
Cho hình bình hành ABCD. Lấy điểm M thuộc cạnh AB và điểm N thuộc cạnh CD sao cho AM = CN. Chứng minh rằng:
a) AN = CM;
Cho ba điểm không thẳng hàng.
a) Tìm một điểm sao cho nó cùng với ba điểm đã cho là bốn đỉnh của một hình bình hành.
Cho hình bình hành ABCD. Lấy điểm E sao cho B là trung điểm của AE, lấy điểm F sao cho C là trung điểm của DF. Chứng minh rằng:
a) Hai tứ giác AEFD, ABFC là những hình bình hành;
Vẽ tứ giác ABCD theo hướng dẫn sau:
Bước 1. Vẽ đoạn thẳng AB và đường thẳng a song song với AB.
Bước 2. Lấy điểm C ∈ a.
Bước 3. Trên a chọn D sao cho CD = AB và A, D nằm cùng phía đối với BC.
Hãy giải thích tại sao tứ giác ABCD là hình bình hành.
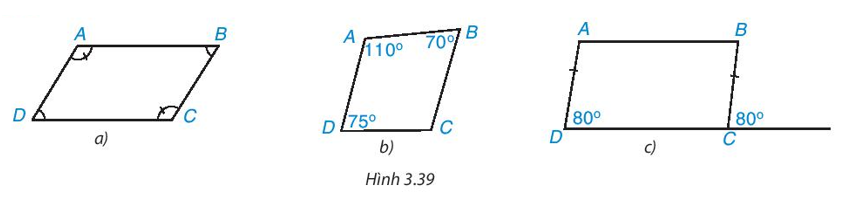
Trong các tứ giác ở Hình 3.39, tứ giác nào là hình bình hành? Vì sao?