Cho hình bình hành ABCD, một đường thẳng đi qua D cắt AC, AB, CB theo thứ tự tại M, N, K. Chứng minh rằng: DM2 = MN . MK.
 Giải bởi Vietjack
Giải bởi Vietjack
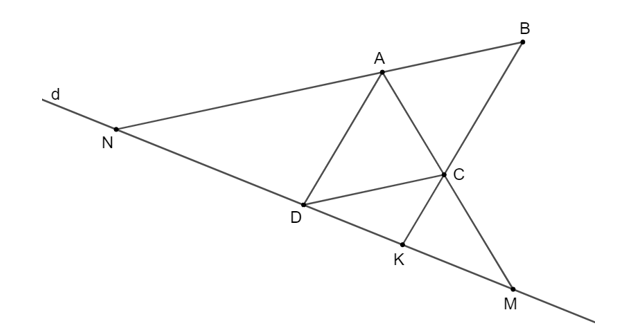
Vì ABCD là hình bình hành nên AB // CD, AD // BC suy ra AN // cD, ad // ck.
Áp dụng định lí Thalès vào tam giác AMN có AN // CD, ta được:
(1)
Áp dụng định lí Thalès vào tam giác ADM có CK // AD, ta được:
(2)
Từ (1) và (2) suy ra: .
Do đó DM2 = MN . MK (đpcm).
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho tam giác ABC, phân giác AD (D ∈ BC). Đường thẳng qua D song song với AB cắt AC tại E. Chứng minh rằng .
Cho tứ giác ABCD, gọi E, F, K lần lượt là trung điểm của AD, BC, AC.
a) Chứng minh EK // CD, FK // AB.
Tam giác ABC có AB = 15 cm, AC = 20 cm, BC = 25 cm. Đường phân giác của góc BAC cắt BC tại D.
a) Tính độ dài đoạn thẳng DB và DC.