Giải SGK Toán 8 KNTT Luyện tập chung trang 87 có đáp án
-
42 lượt thi
-
7 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
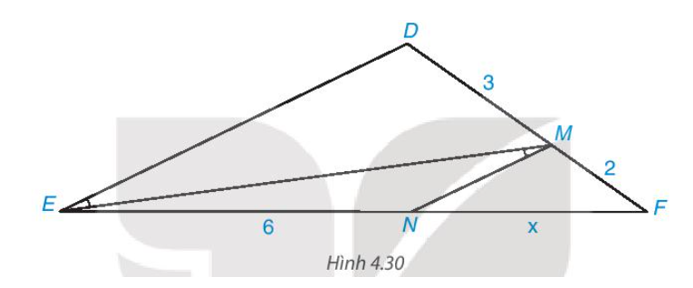
Tìm độ dài x trong Hình 4.30
 Xem đáp án
Xem đáp án
Trong Hình 4.30 có mà hai góc này ở vị trí so le trong nên MN // DE.
Áp dụng định lí Thalès vào tam giác DEF có MN // DE, ta có:
hay .
Suy ra (đvđd).
Vậy x = 4 (đvđd).
Câu 2:
Cho tứ giác ABCD, gọi E, F, K lần lượt là trung điểm của AD, BC, AC.
a) Chứng minh EK // CD, FK // AB.
 Xem đáp án
Xem đáp án
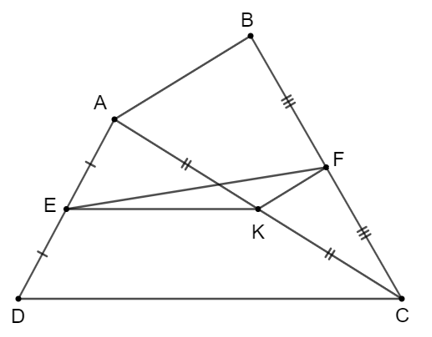
a) Vì E, K lần lượt là trung điểm của AD, AC nên EK là đường trung bình của tam giác ACD suy ra EK // CD.
Vì K, F lần lượt là trung điểm của AC, BC nên KF là đường trung bình của tam giác ABC suy ra KF // AB.
Vậy EK // CD, FK // AB.
Câu 3:
b) So sánh EF và .
 Xem đáp án
Xem đáp án
b) Vì EK là đường trung bình của tam giác ACD nên ;
Vì KF là đường trung bình của tam giác ABC nên .
Do đó (1)
Áp dụng bất đẳng thức tam giác vào tam giác KEF, ta có: EF < EK + KF (2)
Từ (1) và (2) ta suy ra .
Câu 4:
Cho tam giác ABC, phân giác AD (D ∈ BC). Đường thẳng qua D song song với AB cắt AC tại E. Chứng minh rằng .
 Xem đáp án
Xem đáp án
Theo đề bài, AD là tia phân giác của , áp dụng tính chất đường phân giác vào tam giác ABC, ta có: (1)
Đường thẳng qua D song song với AB cắt AC tại E hay DE // AB, áp dụng định lí Thalès vào tam giác ABC, ta có: (2)
Từ (1) và (2) suy ra (đpcm).
Câu 5:
Tam giác ABC có AB = 15 cm, AC = 20 cm, BC = 25 cm. Đường phân giác của góc BAC cắt BC tại D.
a) Tính độ dài đoạn thẳng DB và DC.
 Xem đáp án
Xem đáp án
a) Áp dụng tính chất đường phân giác, ta có:
.
Suy ra .
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
.
Do đó, (cm); (cm).
Vậy cm; cm.
Câu 6:
b) Tính tỉ số diện tích của hai tam giác ABD và ACD.
 Xem đáp án
Xem đáp án
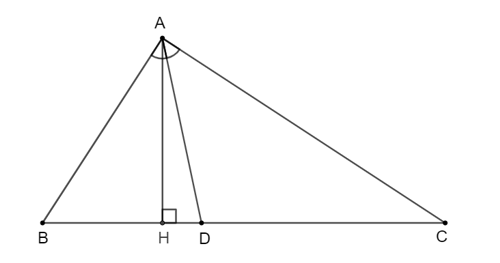
) Hai tam giác ABD và ACD có chung đường cao kẻ từ đỉnh A đến cạnh BC, ta gọi đường cao đó là AH.
Ta có: .
Suy ra .
Vậy tỉ số diện tích của hai tam giác ABD và ACD bằng .
Câu 7:
Cho hình bình hành ABCD, một đường thẳng đi qua D cắt AC, AB, CB theo thứ tự tại M, N, K. Chứng minh rằng: DM2 = MN . MK.
 Xem đáp án
Xem đáp án
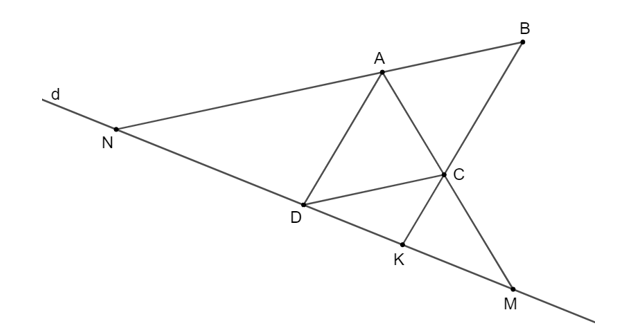
Vì ABCD là hình bình hành nên AB // CD, AD // BC suy ra AN // cD, ad // ck.
Áp dụng định lí Thalès vào tam giác AMN có AN // CD, ta được:
(1)
Áp dụng định lí Thalès vào tam giác ADM có CK // AD, ta được:
(2)
Từ (1) và (2) suy ra: .
Do đó DM2 = MN . MK (đpcm).
