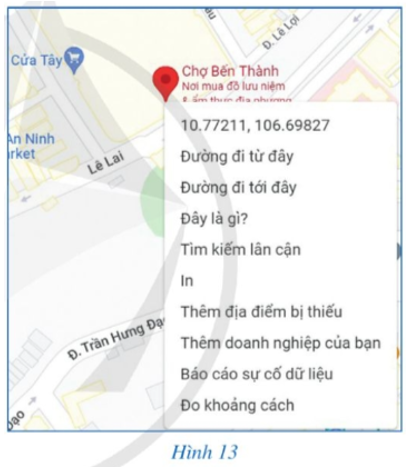
Nhập cụm từ “chợ Bến Thành” trên trang http://google.com/maps, sau đó nháy chuột vào địa điểm đó trên bản đồ ta được thông tin về kinh độ, vĩ độ như Hình 13. Hãy viết tọa độ địa lí của chợ Bến Thành thuộc Thành phố Hồ Chí Minh.

Trong mặt phẳng tọa độ Oxy, nêu cách xác định điểm A(– 3; – 5).

b) Điểm thuộc trục hoành có hoành độ bằng 0.

Cho tam giác ABC như Hình 12.

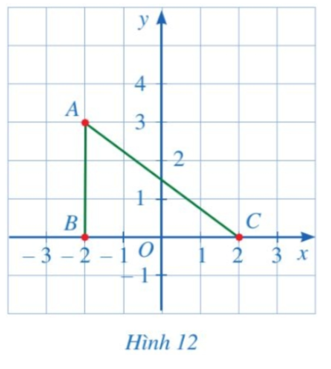
a) Xác định tọa độ các điểm A, B, C.

Ở lớp 6, ta đã biết rằng mỗi điểm trên bản đồ địa lí được xác định bởi một cặp gồm hai con số (tọa độ địa lí) là kinh độ và vĩ độ. Chẳng hạn, tọa độ địa lí của hồ Hoàn Kiếm ở Thủ đô Hà Nội là: (21°01’B; 105°51’Đ).

Trong toán học, cặp số để xác định vị trí của một điểm trên mặt phẳng được gọi là gì?

Cho điểm M trong mặt phẳng tọa độ Oxy (Hình 6).

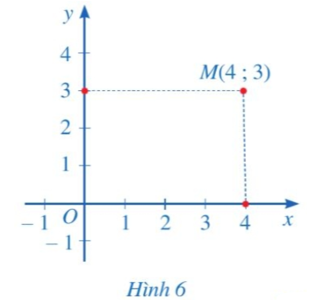
a) Hình chiếu của điểm M trên trục hoành Ox là điểm nào trên trục số Ox?

Xác định tọa độ điểm A trong mỗi trường hợp sau:

a) Hoành độ bằng – 3 và tung độ bằng 5;

Điểm M(a; b) thuộc góc phần tư nào trong mỗi trường hợp sau?

a) a > 0, b > 0.

c) Điểm thuộc trục tung có tung độ bằng 0.

b) Trong mặt phẳng tọa độ Oxy, biểu diễn các điểm có tọa độ là các cặp số (x; y) tương ứng ở bảng đã viết ở câu a.

Số lượng sản phẩm bán được y (nghìn sản phẩm) là một hàm số theo thời gian x (tháng). Hàm số này được biểu thị dưới dạng Bảng 2.

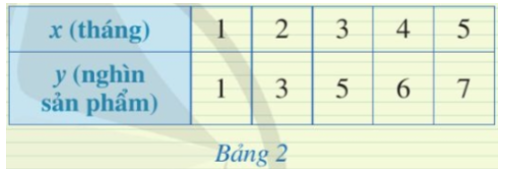
Trong mặt phẳng tọa độ Oxy, hai điểm A(2; 3), B(5; 6) có thuộc đồ thị của hàm số hay không? Vì sao?

d) Điểm thuộc trục tung có hoành độ bằng 0.

c) Trong mặt phẳng tọa độ Oxy, điểm M(15; 24) có thuộc đồ thị của hàm số cho bởi bảng trên hay không? Vì sao?

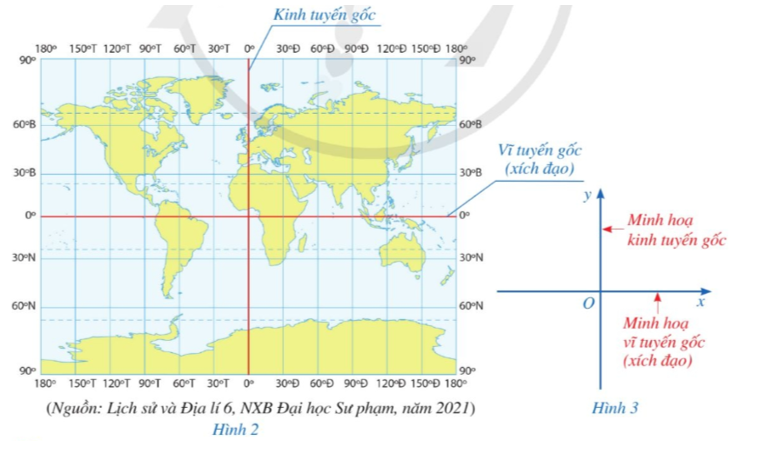
Hình 2 là một dạng phép chiếu bản đồ có các đường kinh tuyến và vĩ tuyến đều là các đường thẳng, trong đó kinh tuyến gốc và vĩ tuyến gốc được minh họa bằng hai đường thẳng màu đỏ. Chúng được biểu diễn bởi hai trục Ox, Oy trên mặt phẳng ở Hình 3. Nêu nhận xét về hai trục Ox, Oy.

Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai?

a) Điểm thuộc trục hoành có tung độ bằng 0.

b) Biểu diễn trong mặt phẳng tọa độ Oxy các điểm M1(x1; y1); M2(x2; y2); M3(x3; y3).