Một con quạ bị khát nước, nó tìm thấy một bình đựng nước hình trụ, do mức nước trong bình chỉ còn lại hai phần ba so với thể tích của bình nên nó không thể thò đầu vào uống nước được. Nó liền gắp 3 viên bi ve hình cầu để sẵn bên cạnh bỏ vào bình thì mực nước dâng lên vừa đủ đầy bình và nó có thể uống nước. Biết 3 viên bi ve hình cầu đều có bán kính là 1cm và chiều cao của bình hình trụ gấp 8 lần bán kính của nó. Diện tích xung quanh của bình hình trụ nói trên gần với số nào nhất trong các số sau

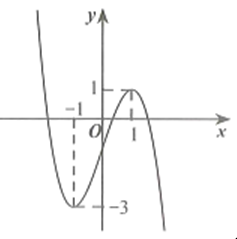
Cho hàm số y=f(x) có đồ thị như hình vẽ. Số nghiệm của phương trình 2|f(x)|-5=0 là:

Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhậtAB=a, BC=2a, SA=a  và SA vuông góc với mặt phẳng đáy. Côsin của góc giữa đường thẳng SD và mặt phẳng (SAC) bằng

Trong không gian Oxyz, cho mặt cầu $\left(S_1\right):{\left(x-1\right)}^2 +y^2 +{\left(z-2\right)}^2=1$ và điểm I(3;-1;4). Phương trình của mặt cầu (S) có tâm I và tiếp xúc ngoài với mặt cầu (S₁) là

Tập nghiệm S của bất phương trình $\ln \left(x^2+1\right)-\ln \left(2x+4\right)>0$.

Cho hàm số $y= \frac{x-2 }{\sqrt{2x^2+1}-3}$. Tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị đã cho là

Đặt $a={\log }_{2}5, b={\log }_{5}3$. Mệnh đề nào dưới đây đúng?

Cho phần vật thể (H) được giới hạn bởi hai mặt phẳng (P) và (Q) vuông góc với trục Ox tại x=0;x=3. Cắt phần vật thể (H) bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ bằng x ($0\le x\le 3$ ) ta được thiết diện là hình chữ nhật có kích thước lần lượt là x và $\sqrt{3-x}$. Thể tích phần vật thể (H) bằng

Cho hàm số f(x) liên tục trên $\mathrm{ℝ}$ thỏa mãn $f\left(2x\right)=3f\left(x\right),\forall x\in \mathrm{ℝ}$. Biết rằng ${\int }_0^{1}f\left(x\right)dx=1$. Tính tích phân ${\int }_1^{2}f\left(x\right)dx$.

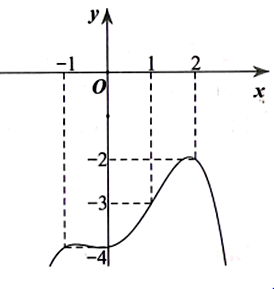
Cho hàm số y=f(x) có đạo hàm liên tục trên $\mathrm{ℝ}$ và đồ thị hàm số y=f'(x) như hình vẽ bên. Bất phương trình $f\left(x\right)\le 3^x-2x+m$ có nghiệm trên $(-\infty ;1]$ khi và chỉ khi

Cho cấp số nhân (u_n). Biết tổng ba số hạng đầu bằng 4, tổng của số hạng thứ tư, thứ năm và thứ sáu bằng -32. Số hạng tổng quát của cấp số nhân là

Cho hình chóp S.ABCD, đáy là hình vuông cạnh bằng a. Gọi M là trung điểm SA. Biết hình chiếu vuông góc của S trùng với trọng tâm G của tam giác ACD, góc giữa đường thẳng SB và mặt phẳng đáy bằng 60^o. Khoảng cách từ M đến mặt phẳng (SBC) bằng

Cho các số thực a, b thỏa mãn đẳng thức $2a+3+\left(3b-2i\right)i=4-3i$ với i là đơn vị ảo. Giá trị biểu thức P=a+b bằng

Cho số phức z thỏa mãn $\left|z-4+\overline{z}+\right|+\left|z-\overline{z}\right|\ge 4$ và số phức $w=\left(z-2i\right)\left(\overline{z}i+2-4i\right)$ có phần ảo là số thực không dương. Trong mặt phẳng tọa độ Oxy, hình phẳng (H) là tập hợp các điểm biểu diễn của số phức z. Diện tích hình (H) gần nhất với số nào sau đây?

Trong không gian Oxyz, cho đường thẳng $d:\frac{x+1}{2}=\frac{y-1}{-1}=\frac{z-2}{-1}$. Gọi $\left(\alpha \right)$ là mặt phẳng chứa đường thẳng d và tạo với mặt phẳng (Oxy) một góc nhỏ nhất. Khoảng cách từ M(0;-3;4) đến mặt phẳng $\left(\alpha \right)$ bằng

Cho khối chóp tam giác S.ABC có $SA=\frac{a}{2}$, đáy là tam giác ABC vuông cân tại A, AB=AC=a. Thể tích khối chóp đã cho bằng