Xét tính chẵn, lẻ của các hàm số:
a) y = sinx cosx;
b) y = tanx + cotx;
c) y = sin2x.
 Giải bởi Vietjack
Giải bởi Vietjack
a) Xét hàm số f(x) = y = sinx cosx có tập xác định D = ℝ:
• ∀x ∈ D thì ‒x ∈ D;
• f(‒x) = sin(‒x) . cos(‒x) = ‒sinx cosx = ‒f(x).
Do đó hàm số y = sinx cosx là hàm số lẻ.
b) Xét hàm số f(x) = y = tanx + cotx có tập xác định \(D = \mathbb{R}\backslash \left\{ {k\pi ;\frac{\pi }{2} + k\pi |k \in \mathbb{Z}} \right\}\):
• ∀x ∈ D thì ‒x ∈ D;
• f(‒x) = tan(‒x) + cot(‒x) = (‒tanx) + (‒cotx) = ‒(tanx + cotx) = ‒f(x).
Do đó hàm số y = tanx + cotx là hàm số lẻ.
c) Xét hàm số f(x) = y = sin2x có tập xác định D = ℝ:
• ∀x ∈ D thì ‒x ∈ D;
• f(‒x) = sin2(‒x) = (‒sinx)2 = sin2x = f(x).
Do đó hàm số y = sin2x là hàm số chẵn.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Dùng đồ thị hàm số, tìm giá trị của x trên khoảng \(\left( { - \pi ;\frac{{3\pi }}{2}} \right)\) để:
Hàm số y = tanx nhận giá trị bằng ‒1;
Dùng đồ thị hàm số, tìm giá trị của x trên đoạn [‒2π; 2π] để:
Hàm số y = sinx nhận giá trị bằng 1;Dùng đồ thị hàm số, tìm giá trị của x trên đoạn [‒2π; 2π] để:
Hàm số y = cosx nhận giá trị bằng ‒1;
Dùng đồ thị hàm số, hãy cho biết:
Với mỗi m ∈ ℝ, có bao nhiêu giá trị \(\alpha \in \left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\) sao cho tanα = m;
Dùng đồ thị hàm số, tìm giá trị của x trên khoảng \(\left( { - \pi ;\frac{{3\pi }}{2}} \right)\) để:
Hàm số y = tanx nhận giá trị bằng 0;
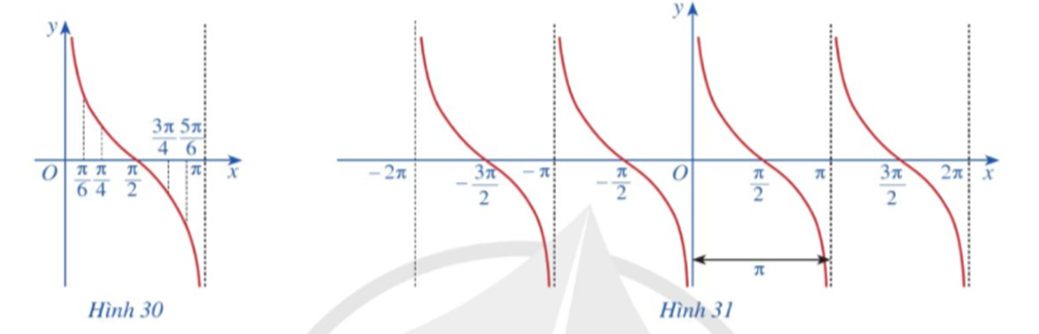
Làm tương tự như trên đối với các khoảng (π; 2π), (‒π; 0), (‒2π; ‒π), …, ta có đồ thị hàm số y = cotx trên E được biểu diễn ở Hình 31.
Dùng đồ thị hàm số, hãy cho biết:
Với mỗi m ∈ ℝ, có bao nhiêu giá trị α ∈ (0; π) sao cho cotα = m.
Dùng đồ thị hàm số, hãy cho biết:
Quan sát đồ thị hàm số y = cotx ở Hình 31.
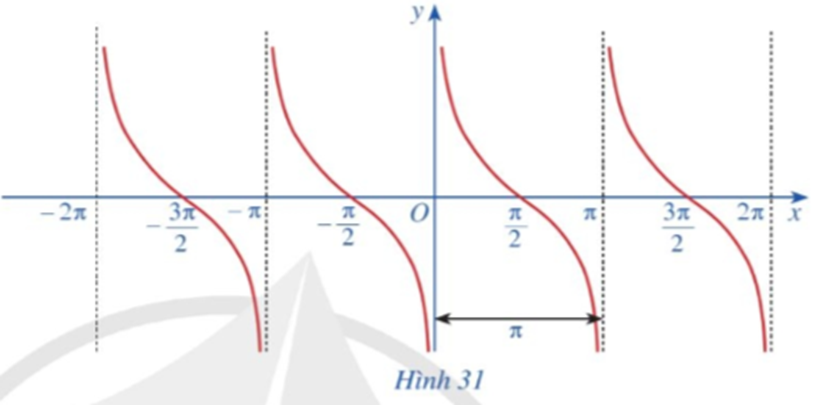
Gốc toạ độ có là tâm đối xứng của đồ thị hàm số không? Từ đó kết luận tính chẵn, lẻ của hàm số y = cotx.
Dùng đồ thị hàm số, tìm giá trị của x trên khoảng \(\left( { - \pi ;\frac{{3\pi }}{2}} \right)\) để:
Hàm số y = cotx nhận giá trị bằng 0.Dùng đồ thị hàm số, tìm giá trị của x trên đoạn [‒2π; 2π] để:
Hàm số y = cosx nhận giá trị bằng 0.
Quan sát đồ thị hàm số y = cotx ở Hình 31.
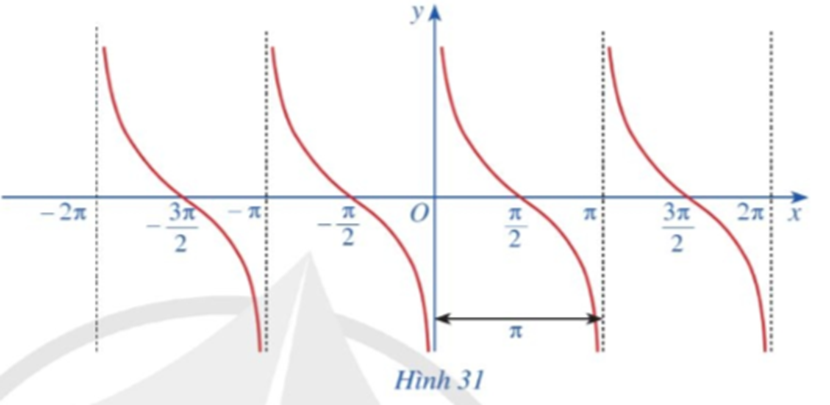
Tìm khoảng đồng biến, nghịch biến của hàm số y = cotx.
Dùng đồ thị hàm số, tìm giá trị của x trên đoạn [‒2π; 2π] để:
Hàm số y = sinx nhận giá trị bằng 0;
Xét sự biến thiên của hàm số sau trên các khoảng tương ứng:
y = cosx trên khoảng (‒20π; ‒19π), (‒9π; ‒8π).
Hàm số y = cosx đồng biến hay nghịch biến trên khoảng (‒2π; ‒π)?