Cho bốn mệnh đề sau:
(I) Nếu hai mặt phẳng và song song với nhau thì mọi đường thẳng nằm trong mặt phẳng đều song song với (II) Hai đường thẳng nằm trên hai mặt phẳng song song thì song song với nhau.
(III) Trong không gian hai đường thẳng không có điểm chung thì chéo nhau. (IV) Có thể tìm được hai đường thẳng song song mà mỗi đường thẳng cắt đồng thời hai đường thẳng chéo nhau cho trước.
Trong các mệnh đề trên có bao nhiêu mệnh đề sai?
A. 4
B. 2
C. 1
D. 3
 Giải bởi Vietjack
Giải bởi Vietjack
Có 3 mệnh đề sai là (II), (III), (IV).
(II) sai vì hai đường thẳng nằm trên hai mặt
phẳng song song thì có thể song song hoặc chéo nhau.
(III) sai vì hai đường thẳng không có điểm chung
thì có thể chéo nhau hoặc song song với nhau.
(IV) sai vì nếu tồn tại hai đường song song mà
mỗi đường thẳng cắt đồng thời hai đường thẳng
chéo nhau cho trước thì cả bốn đường đó sẽ đồng
phẳng (mâu thuẫn với dữ kiện hai đường thẳng ban đầu chéo nhau).
Đáp án cần chọn là: D
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O, gọi I là trung điểm cạnh SC. Mệnh đề nào sau đây sai?
Cho hình chóp S.ABCD có đáy là hình thang đáy lớn là CD. Gọi M là trung điểm của cạnh SA, N là giao điểm của cạnh SB và mặt phẳng (MCD). Mệnh đề nào sau đây là mệnh đề đúng?
Cho hình chóp S.ABCD có đáy là hình bình hành. Giao tuyến của (SAB) và (SCD) là
Cho hình chóp S.ABCD có đáy là hình chữ nhật. Mặt phẳng (P) cắt các cạnh SA, SB, SC, SD lần lượt tại M, N, P, Q. Gọi I là giao điểm của MQ và NP. Câu nào sau đây đúng?
Cho tứ diện ABCD. Gọi M là một điểm bất kì nằm trên đoạn AC (khác A và C). Mặt phẳng (P) qua M và song song với các đường thẳng AB, CD. Thiết diện của (P) với tứ diện đã cho là hình gì?
Cho tứ diện ABCD. Gọi M, N lần lượt là trọng tâm của các tam giác ABC, ABD. Những khẳng định nào sau là đúng?
(1) : MN // (BCD )
(2) : MN // (ACD )
(3) : MN // ( ABD)
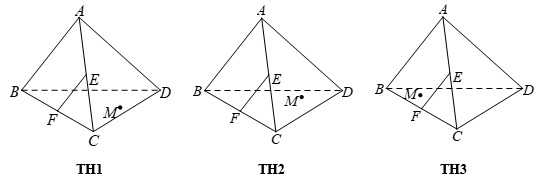
Cho tứ diện ABCD. Gọi E, F lần lượt là trung điểm của các cạnh AC và BC. Trên mặt phẳng (BCD) lấy một điểm M tùy ý (điểm M có đánh dấu tròn như hình vẽ). Nêu đầy đủ các trường hợp (TH) để thiết diện tạo bởi mặt phẳng (MEF) với tứ diện ABCD là một tứ giác.
Cho tứ diện ABCD, G là trọng tâm tứ diện. Gọi là giao điểm của AG và mặt phẳng (BCD), là giao điểm của BG và mặt phẳng (ACD). Khẳng định nào sau đây là đúng?
Cho hình chóp S.ABCD có đáy là hình thoi cạnh 3a, SA = SD = 3a, . Gọi M, N lần lượt là trung điểm của các cạnh SA và SD, (P) là điểm thuộc cạnh AB sao cho AP = 2a. Tính diện tích thiết diện của hình chóp khi cắt bởi mặt phẳng (MNP).
Cho tứ diện ABCD. Gọi G và E lần lượt là trọng tâm của tam giác ABD và ABC. Mệnh đề nào dưới đây đúng
Trong không gian cho bốn điểm không đồng phẳng. Có thể xác định được bao nhiêu mặt phẳng phân biệt từ các điểm đã cho?