Cho hàm số . Khẳng định nào sau đây đúng nhất?
A. Hàm số liên tục tại x=1và x= −1
B. Hàm số liên tục tại x=1, không liên tục tại điểm x= −1
C. Hàm số không liên tục tại x=1 và x=−1
D. Tất cả đều sai
 Giải bởi Vietjack
Giải bởi Vietjack
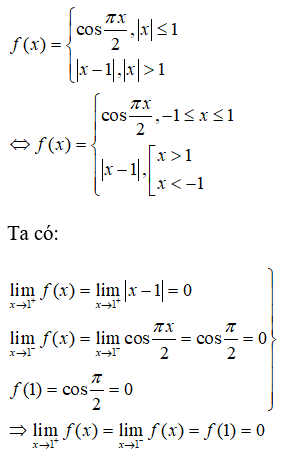

Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Giá trị thực của tham số m để hàm số liên tục tại x=0 thỏa mãn điều kiện nào dưới đây?
Tính tổng (S ) gồm tất cả các giá trị m để hàm số liên tục tại x=1.
Biết rằng . Tìm giá trị thực của tham số m để hàm số liên tục tại x=1
Biết rằng . Tìm giá trị thực của tham số m để hàm số liên tục tại
Cho a và b là các số thực khác 0. Tìm hệ thức liên hệ giữa a và b để hàm số liên tục tại x = 0.
Cho hàm số . Hàm số y=f(x) liên tục trên các khoảng nào sau đây?
Biết rằng liên tục trên đoạn (0;1) (với a là tham số). Khẳng định nào dưới đây về giá trị a là đúng?
I. HÀM SỐ LIÊN TỤC TẠI MỘT ĐIỂM
Định nghĩa 1
Cho hàm số y = f(x) xác định trên khoảng K và ∈ K.
Hàm số y = f(x) được gọi là liên tục tại x0 nếu
Ví dụ 1. Xét tính liên tục của hàm số tại = 2.
Giải
Hàm số đã cho xác định trên .
Do đó hàm số xác định trên khoảng chứa = 2. Khi đó ta có:
.
Vậy hàm số y = f(x) liên tục tại = 2.
II. HÀM SỐ LIÊN TỤC TRÊN MỘT KHOẢNG
Định nghĩa 2
Hàm số y = f(x) được gọi là liên tục trên một khoảng nếu nó liên tục tại mọi điểm của khoảng đó.
Hàm số y = f(x) được gọi là liên tục trên đoạn [a; b] nếu nó liên tục trên khoảng (a; b) và
Nhận xét: Đồ thị của hàm số liên tục trên một khoảng là một đường liền trên khoảng đó.
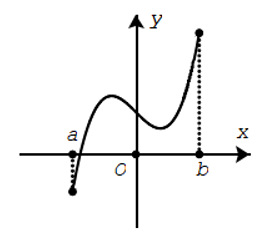
Hàm số liên tục trên khoảng (a;b)
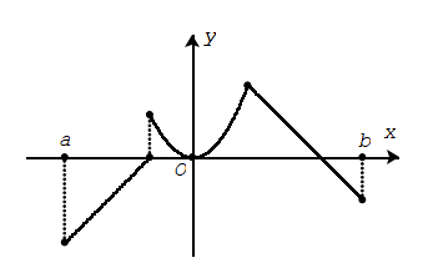
Hàm số không liên tục trên khoảng (a; b).
III. MỘT SỐ ĐỊNH LÍ CƠ BẢN
Định lí 1
a) Hàm số đa thức liên tục trên toàn bộ tập số thực .
b) Hàm số phân thức hữu tỉ và hàm số lượng giác liên tục trên từng khoảng xác định của chúng.
Định lí 2
Giả sử y = f(x) và y = g(x) là hai hàm số liên tục tại điểm x0. Khi đó:
a) Các hàm số y = f(x) + g(x), y = f(x) – g(x) và y = f(x).g(x) liên tục tại x0;
b) Hàm số liên tục tại x0 nếu g(x0) ≠ 0.
Ví dụ 2. Cho hàm số trên tập xác định của nó.
Giải
Tập xác định
- Nếu x = 3, ta có f(3) = 4,
Do đó f(x) liên tục tại x = 3.
- Nếu thì là hàm phân thức hữu tỉ nên liên tục trên các khoảng .
Vậy hàm số y = f(x) liên tục trên .
Định lí 3
Nếu hàm số y = f(x) liên tục trên đoạn [a;b] và f(a).f(b) < 0, thì tồn tại ít nhất một điểm c ∈ (a; b) sao cho f(c) = 0.
Định lí 3 có thể phát biểu theo một dạng khác như sau:
Nếu hàm số y = f(x) liên tục trên đoạn [a; b] và f(a).f(b) < 0, thì phương trình f(x) = 0 có ít nhất một nghiệm nằm trong khoảng (a, b).
Ví dụ 3. Chứng minh rằng phương trình x5 – 3x – 7 = 0 luôn có nghiệm.
Giải
Xét hàm f(x) = x5 – 3x – 7
Ta có: f(0) = - 7, f(2) = 19. Do đó f(0).f(2) = (-7).19 < 0.
Vì hàm số f(x) là hàm đa thức nên liên tục trên . Do đó hàm số f(x) liên tục trên [0;2]. Từ đó suy ra phương trình f(x) = 0 có ít nhất một nghiệm .
Vậy phương trình đã cho luôn có nghiệm.