Cho các khẳng định sau:
(I): Phép chia đa thức + 5 cho đa thức 3x – 2 là phép chia hết
(II): Phép chia đa thức ( – 2x + 3) cho đa thức ( – x + 1) là phép chia hết
Chọn câu đúng
A. Cả (I) và (II) đều đúng
B. Cả (I) và (II) đều sai
C. (I) đúng, (II) sai
D. (I) sai, (II) đúng
 Giải bởi Vietjack
Giải bởi Vietjack
Lời giải
Ta có
Vì phần dư R = 5 ≠ 0 nên phép chia đa thức + 5 cho đa thức 3x – 2 là phép chia có dư. Do đó (I) sai
Lại có
Nhận thấy phần dư R = 0 nên phép chia đa thức ( – 2x + 3) cho đa thức (2 – x + 1) là phép chia hết. Do đó (II) đúng
Đáp án cần chọn là: D
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Có bao nhiêu giá trị của a để đa thức – 6x – 2a chia hết cho đa thức x + 1.
Tìm a và b để đa thức f(x) = + ax + b chia hết cho đa thức g(x) = – x – 2
Phép chia đa thức ( – 2x + 1) cho đa thức + 1 được đa thức dư là:
Phần dư của phép chia đa thức – 3x + 1 cho đa thức + 1 có hệ số tự do là
Tìm giá trị của a và b đề đa thức 4 + ax + b chia cho đa thức – 1 dư 2x – 3.
Thương của phép chia đa thức ( – 8) cho đa thức ( – 2) có hệ số tự do là
Cho các khẳng định sau:
(I): Phép chia đa thức ( – 26x – 24) cho đa thức + 4x + 3 là phép chia hết
(II): Phép chia đa thức ( – 7x + 6) cho đa thức x + 3 là phép chia hết
Chọn câu đúng
Biết đa thức + a + b chia hết cho – x + 1. Khi đó, khẳng định nào sau đây là đúng.
Biết phần dư của phép chia đa thức ( + 2) cho đa thức ( + 1) là số tự nhiên a. Chọn câu đúng.
1. Phép chia hết:
- Phép chia hết là phép chia có đa thức dư bằng 0.
Quy tắc chia:
+ Sắp xếp các đa thức theo thứ tự giảm dần của biến.
+ Lấy hạng tử cao nhất của đa thức bị chia chia cho hạng tử cao nhất của đa thức chia ta được thương 1.
+ Nhân thương 1 với đa thức chia và lấy đa thức bị chia trừ đi tích đó.
+ Lấy hạng tử cao nhất của đa thức vừa tìm được chia cho hạng tử cao nhất đa thức chia ta được thương 2.
+ Tiếp tục lặp lại các bước trên đến khi nhận được hiệu bằng 0.
Ví dụ 1: Làm tính chia:
Lời giải:
Ta có:
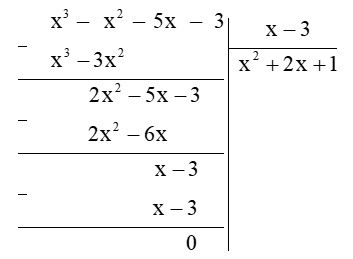
Vậy .
2. Phép chia có dư:
- Phép chia có dư là phép chia có đa thức dư khác 0.
Quy tắc chia: Làm tương tự phép chia hết đến khi thu được đa thức dư có bậc nhỏ hơn bậc của đa thức chia.
Chú ý: Với hai đa thức tùy ý A và B của cùng một biến (B ≠ 0), tồn tại duy nhất một cặp đa thức Q và R sao cho A = B.Q + R, trong đó R = 0 hoặc bậc của R nhỏ hơn bậc của B (R được gọi là dư trong phép chia A cho B).
Khi R = 0 phép chia A cho B là phép chia hết.
Ví dụ 2: Làm tính chia: .
Lời giải:
Ta có:
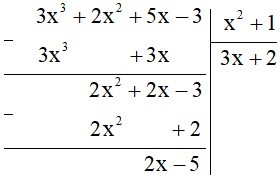
Vậy
Hay .