Cho tam giác ABC cân tại A. Trên cạnh AC lấy điểm M, trên đoạn thẳng BM lấy điểm K sao cho góc . Tính MB.MK bằng
A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack
Vì ΔMBC ~ ΔMCK nên (hai cạnh tương ứng tỉ lệ)
Suy ra = MB.MK
Đáp án: C
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho hình bình hành ABCD, điểm F trên cạnh BC. Tia AF cắt BD và DC lần lượt ở E và G. Chọn khẳng định sai.
Cho ΔABC có các đường cao BD và CE cắt nhau tại H. Gọi M là giao của AH với BC. Chọn khẳng định sai.
Cho tam giác ABC cân tại A. Trên cạnh AC lấy điểm M, trên đoạn thẳng BM lấy điểm K sao cho góc . Tam giác MBC đồng dạng với tam giác
Cho tam giác ABC vuông tại A có: AB = 5, AC = 12. Trên cạnh BC lấy điểm M sao cho BM = BC. Qua M kẻ đường thẳng vuông góc với AC tại N. Độ dài MN là:
Cho hai tam giác ABC và tam giác FED có , cần thêm điều kiện gì dưới đây để hai tam giác (thứ tự đỉnh như vậy) đồng dạng theo trường hợp góc - góc?
Cho ΔABC cân tại A, có BC = 2a, M là trung điểm BC, lấy D, E thuộc AB, AC sao cho . Tính BD.CE bằng
Cho ΔABC có các đường cao BD và CE cắt nhau tại H. Gọi M là giao của AH với BC. Chọn câu đúng.
Cho hình thang vuông ABCD ( = ) có BCBD, AB = 4cm, CD = 9cm. Độ dài BD là:
Cho ΔABC có đường cao AD, CE và trực tâm H. Chọn khẳng định sai.
Cho hình bình hành ABCD có I là giao điểm của AC và BD. E là một điểm bất kì thuộc BC, qua E kẻ đường thẳng song song với AB và cắt BD, AC, AD tại G, H, F. Chọn kết luận sai?
Cho ΔABC cân tại A, có BC = 2a, M là trung điểm BC, lấy D, E thuộc AB, AC sao cho . Góc BDM bằng với góc nào dưới đây?
Cho ΔABC có đường cao AD, CE và trực tâm H. Chọn câu trả lời đúng nhất.
1. Định lí
- Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng với nhau.
- Ví dụ 1. Cho tam giác ABC và các đường cao BH, CK. Chứng minh ∆ABH ∆ ACK.
Lời giải:
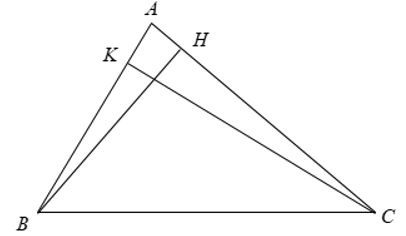
Xét ∆ABH và ∆ACK có:
Suy ra: ∆ABH ∆ ACK.