Cho ΔABC có các đường cao BD và CE cắt nhau tại H. Gọi M là giao của AH với BC. Chọn khẳng định sai.
A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack
Theo cmt ta có: ΔHBE ~ ΔHCD
Xét ΔHED và ΔHBC ta có:
(chứng minh trên)
(hai góc đối đỉnh)
=> ΔHED ~ ΔHBC (c - g - c)
(1)
Mà đường cao BD và CE cắt nhau tại H (theo giả thiết)
=> H là trực tâm của ΔABC
=> AH vuông góc với BC tại M => =
Xét ΔAMB và ΔCEB có:
chung
=> ΔAMB ~ ΔCEB (g - g)
hay (2)
Từ (1) và (2) ta có: nên A, B, C đúng, D sai.
Đáp án: D
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho hình bình hành ABCD, điểm F trên cạnh BC. Tia AF cắt BD và DC lần lượt ở E và G. Chọn khẳng định sai.
Cho tam giác ABC cân tại A. Trên cạnh AC lấy điểm M, trên đoạn thẳng BM lấy điểm K sao cho góc . Tam giác MBC đồng dạng với tam giác
Cho tam giác ABC vuông tại A có: AB = 5, AC = 12. Trên cạnh BC lấy điểm M sao cho BM = BC. Qua M kẻ đường thẳng vuông góc với AC tại N. Độ dài MN là:
Cho hai tam giác ABC và tam giác FED có , cần thêm điều kiện gì dưới đây để hai tam giác (thứ tự đỉnh như vậy) đồng dạng theo trường hợp góc - góc?
Cho ΔABC cân tại A, có BC = 2a, M là trung điểm BC, lấy D, E thuộc AB, AC sao cho . Tính BD.CE bằng
Cho ΔABC có các đường cao BD và CE cắt nhau tại H. Gọi M là giao của AH với BC. Chọn câu đúng.
Cho hình thang vuông ABCD ( = ) có BCBD, AB = 4cm, CD = 9cm. Độ dài BD là:
Cho ΔABC có đường cao AD, CE và trực tâm H. Chọn khẳng định sai.
Cho hình bình hành ABCD có I là giao điểm của AC và BD. E là một điểm bất kì thuộc BC, qua E kẻ đường thẳng song song với AB và cắt BD, AC, AD tại G, H, F. Chọn kết luận sai?
Cho tam giác ABC cân tại A. Trên cạnh AC lấy điểm M, trên đoạn thẳng BM lấy điểm K sao cho góc . Tính MB.MK bằng
Cho ΔABC cân tại A, có BC = 2a, M là trung điểm BC, lấy D, E thuộc AB, AC sao cho . Góc BDM bằng với góc nào dưới đây?
Cho ΔABC có đường cao AD, CE và trực tâm H. Chọn câu trả lời đúng nhất.
1. Định lí
- Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng với nhau.
- Ví dụ 1. Cho tam giác ABC và các đường cao BH, CK. Chứng minh ∆ABH ∆ ACK.
Lời giải:
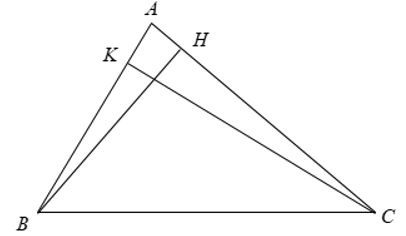
Xét ∆ABH và ∆ACK có:
Suy ra: ∆ABH ∆ ACK.