Cho hàm số $f\left(x\right)=\sqrt{3x^2-1}$. Khẳng định nào sau đây đúng nhất.

1. GIỚI HẠN HỮU HẠN CỦA DÃY SỐ

+) Ta nói dãy số (un) có giới hạn là 0 khi n dần tới dương vô cực, nếu |un| có thể nhỏ hơn một số dương bé tuỳ ý, kể từ một số hạng nào đó trở đi.

Kí hiệu:  $\underset{n\to +\infty }{\lim }{u}_n=0$  hay un → 0 khi n → +∞.

+) Ta nói dãy số (vn) có giới hạn là a (hay vn dần tới a) khi n → +∞ nếu $\underset{n\to +\infty }{\lim }\left(v_n-a\right)=0$

Kí hiệu: $\underset{n\to +\infty }{\lim }{v}_n=a$  hay vn → a khi n → +∞.

Một vài giới hạn đặc biệt

a) $\underset{n\to +\infty }{\lim }\frac{1}{n}=\mathrm{0,}\underset{n\to +\infty }{\lim }\frac{1}{n^k}=0$ với k nguyên dương;

b)  $\underset{n\to +\infty }{\lim }{q}^n$ nếu |q| < 1;

c) Nếu un = c (c là hằng số) thì $\underset{n\to +\infty }{\lim }{u}_n=\underset{n\to +\infty }{\lim }c=c$ .

Chú ý: Từ nay về sau thay cho $\underset{n\to +\infty }{\lim }{u}_n=a$  ta viết tắt là lim un = a.

II. ĐỊNH LÝ VỀ GIỚI HẠN HỮU HẠN

+) Định lí 1

a) Nếu lim un = a và lim vn = b thì

lim (un + vn) = a + b

lim (un – vn) = a – b

lim (un.vn) = a.b

$\lim \frac{u_n}{v_n}=\frac{a}{b}$ (nếu $b\ne 0$)

Nếu $u_n\ge 0$ với mọi n và limun­ = a thì:

$\lim \sqrt{u_n}=\sqrt{a}$ và $a\ge 0.$

III. TỔNG CỦA CẤP SỐ NHÂN LÙI VÔ HẠN

Cấp số nhân vô hạn (un) có công bội q, với |q| < 1 được gọi là cấp số nhân lùi vô hạn.

Tổng của cấp số nhân lùi vô hạn:

$S=u_1+u_2+u_3+\mathrm{...}+u_n+\mathrm{...}=\frac{u_1}{1-q}\left(\left|q\right|<1\right)$

IV. GIỚI HẠN VÔ CỰC

1. Định nghĩa

- Ta nói dãy số (un) có giới hạn là +∞ khi n → +∞, nếu un có thể lớn hơn một số dương bất kì, kể từ một số hạng nào đó trở đi.

Kí hiệu: lim un = +∞ hay un → +∞ khi n → +∞.

- Dãy số (un) có giới hạn là –∞ khi n → +∞, nếu lim (–un) = +∞.

Kí hiệu: lim un = –∞ hay un → –∞ khi n → +∞.

Nhận xét: un = +∞ ⇔ lim(–un) = –∞

2. Một vài giới hạn đặc biệt

Ta thừa nhận các kết quả sau

a) lim nk = +∞ với k nguyên dương;

b) lim qn = +∞ nếu q > 1.

3. Định lí 2

a) Nếu lim un = a và lim vn = ±∞ thì $\lim \frac{u_n}{v_n}=0$

b) Nếu lim un = a > 0, lim vn = 0 và vn > 0, ∀ n > 0 thì $\lim \frac{u_n}{v_n}=+\infty$

c) Nếu lim un = +∞ và lim vn = a > 0 thì $\lim u_n.v_n=+\infty$.

V. GIỚI HẠN HỮU HẠN CỦA HÀM SỐ TẠI MỘT ĐIỂM

1. Định nghĩa

Cho khoảng K chứa điểm x0 và hàm số y = f(x) xác định trên K hoặc trên K \ {x0}.

Ta nói hàm số y = f(x) có giới hạn là số L khi x dần tới x0 nếu với dãy số (xn) bất kì, xn  $\in$K \{x0} và xn → x0, ta có f(xn) → L.

Kí hiệu: $\underset{x\to \infty }{\lim }f\left(x\right)=L$  hay f(x) → L khi x → x0.

Nhận xét: $\underset{x\to \infty }{\lim }x=x_0,\underset{x\to \infty }{\lim }c=c$  với c là hằng số.

2. Định lí về giới hạn hữu hạn

Định lí 1

a) Giả sử $\underset{x\to x_0}{\lim }f\left(x\right)=L$ và $\underset{x\to x_0}{\lim }g\left(x\right)=M$. Khi đó:

$\underset{x\to x_0}{\lim }\left[f\left(x\right)+g\left(x\right)\right]=L+M;$

$\underset{x\to x_0}{\lim }\left[f\left(x\right)-g\left(x\right)\right]=L-M;$

$\underset{x\to x_0}{\lim }f\left(x\right).g\left(x\right)=L.M;$

$\underset{x\to x_0}{\lim }\frac{f\left(x\right)}{g\left(x\right)}=\frac{L}{M}\left(M\ne 0\right);$

b) Nếu $f\left(x\right)\ge 0$ và $\underset{x\to x_0}{\lim }f\left(x\right)=L$ thì $L\ge 0$ và $\underset{x\to x_0}{\lim }\sqrt{f\left(x\right)}=\sqrt{L}.$

(Dấu của f(x) được xét trên khoảng đang tìm giới hạn với $x\ne x_0$).

3. Giới hạn một bên

Định nghĩa 2

- Cho hàm số y = f(x) xác định trên (x0; b).

Số L được gọi là giới hạn bên phải của hàm số y = f(x) khi x → x0 nếu với dãy số (xn) bất kì, x0 < xn < b và xn → x0, ta có f(xn) → L.

Kí hiệu:$\underset{x\to x_0^{+}}{\lim }f\left(x\right)=L$ .

- Cho hàm số y = f(x) xác định trên (a; x0).

Số L được gọi là giới hạn bên trái của hàm số y = f(x) khi x → x0 nếu với dãy số (xn) bất kì, a < xn < x0 và xn → x0, ta có f(xn) → L.

Kí hiệu:$\underset{x\to x_0^{-}}{\lim }f\left(x\right)=L$  .

Định lí 2

$\underset{x\to x_0}{\lim }f\left(x\right)=L\iff \underset{x\to x_0^{+}}{\lim }f\left(x\right)=\underset{x\to x_0^{-}}{\lim }f\left(x\right)=L$

VI. GIỚI HẠN HỮU HẠN CỦA HÀM SỐ TẠI VÔ CỰC

Định nghĩa 3

a) Cho hàm số y = f(x) xác định trên (a; +∞).

Ta nói hàm số y = f(x) có giới hạn là số L khi x → +∞ nếu với dãy số (xn) bất kì, xn > a và xn → +∞, ta có f(xn) → L.

Kí hiệu:$\underset{x\to +\infty }{\lim }f\left(x\right)=L$

b) Cho hàm số y = f(x) xác định trên (–∞; a).

Ta nói hàm số y = f(x) có giới hạn là số L khi x → –∞ nếu với dãy số (xn) bất kì, xn < a và xn → –∞, ta có f(xn) → L.

Kí hiệu:$\underset{x\to -\infty }{\lim }f\left(x\right)=L$

Chú ý:

a) Với c, k là hằng số và k nguyên dương, ta luôn có:

$\underset{x\to +\infty }{\lim }c=c;\underset{x\to -\infty }{\lim }c=c;\underset{x\to +\infty }{\lim }\frac{c}{x^k}=0;\underset{x\to -\infty }{\lim }\frac{c}{x^k}=0.$

b) Định lí 1 về giới hạn hữu hạn của hàm số khi x → x0 vẫn còn đúng khi xn → +∞ hoặc x → –∞

VII. GIỚI HẠN VÔ CỰC CỦA HÀM SỐ

1. Giới hạn vô cực

Định nghĩa 4

Cho hàm số y = f(x) xác định trên (a; +∞).

Ta nói hàm số y = f(x) có giới hạn là –∞ khi x → +∞ nếu với dãy số (xn) bất kì, xn > a và xn → +∞, ta có f(xn) → –∞

Kí hiệu:$\underset{x\to \infty }{\lim }f\left(x\right)=-\infty$

Nhận xét: $\underset{x\to +\infty }{\lim }f\left(x\right)=+\infty \iff \underset{x\to +\infty }{\lim }\left(-f\left(x\right)\right)=-\infty$.

2. Một vài giới hạn đặc biệt

a)  $\underset{x\to +\infty }{\lim }{x}^k=+\infty$ với k nguyên dương.

b) Nếu k chẵn thì $\underset{x\to -\infty }{\lim }{x}^k=+\infty$;

Nếu k lẻ thì $\underset{x\to -\infty }{\lim }{x}^k=-\infty$.

3. Một vài quy tắc về giới hạn vô cực

a) Quy tắc tìm giới hạn của tích f(x).g(x)

b) Quy tắc tìm giới hạn của thương $\frac{f\left(x\right)}{g\left(x\right)}$

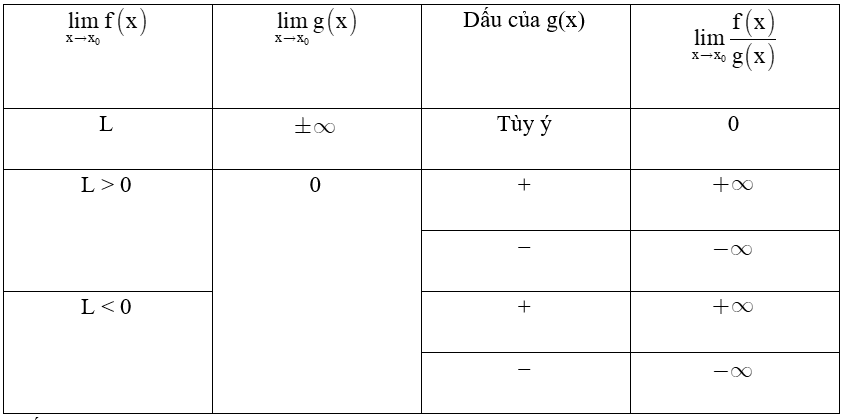
(Dấu của g(x) xét trên một khoảng K nào đó đang tính giới hạn, với $x\ne x_0$)

Chú ý: Các quy tắc trên vẫn đúng cho các trường hợp:

$x\to x_0^{+},x\to x_0^{-};x\to +\infty ;x\to -\infty .$