Đạo hàm của hàm số : bằng biểu thức nào dưới đây?
A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack
Chọn D
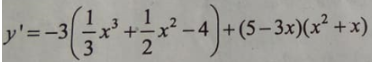
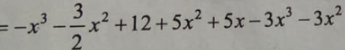
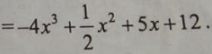
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
I. Đạo hàm của một hàm số thường gặp
1. Định lý 1
Hàm số y = x^n có đạo hàm tại mọi và (x^n)’ = n.x^n-1.
2. Định lý 2
Hàm số có đạo hàm tại mọi x dương và .
Ví dụ 1.
a) Tính đạo hàm y = x^3;
b) Tính đạo hàm tại x = 5.
Lời giải
a) Ta có: y’ = 3x^2;
b) Ta có:
Đạo hàm của hàm số tại x = 5 là:
II. Đạo hàm của tổng, hiệu, tích, thương
1. Định lí 3
Giả sử u = u(x), v = v(x) là các hàm số có đạo hàm tại điểm x thuộc khoảng xác định, ta có:
(u + v)’ = u’ + v’;
(u – v)’ = u’ – v’;
(uv)’ = u’.v + u.v’;
.
2. Hệ quả
Hệ quả 1. Nếu k là một hằng số thì (ku)’ = k.u’.
Hệ quả 2.
Ví dụ 2. Tính đạo hàm của các hàm số sau:
a) y = x5 – 2x2 + 3x + 6;
b) y = (x2 + 1)(2x – 3);
c) .
Lời giải
a) y = x5 – 2x2 + 3x
y’ = (x5 – 2x2 + 3x)’
= (x5)’ – (2x2)’ + (3x)’
= 5x4 – 4x + 3.
b) y = (x2 + x).2x
y’ = (x2 + x)’.2x + (x2 + 1)(2x)’
= [(x2)’ + x’].2x + (x2 + 1).2
= (2x + 1).2x + 2x2 + 2
= 4x2 + 2x + 2x2 + 2
= 6x2 + 2x + 2.
c)
.
III. Đạo hàm hàm hợp
Định lý 4. Nếu hàm số u = g(x) có đạo hàm x là và hàm số y = f(u) có đạo hàm tại u là thì hàm hợp y = f(g(x)) có đạo hàm tại x là: .
Ví dụ 3. Tính đạo hàm của hàm số:
Lời giải
Đặt thì
.