Giải bóng chuyền quốc tế VTV Cup có 8 đội tham gia, trong đó có hai đội Việt Nam. Ban tổ chức bốc thăm ngẫu nhiên để chia thành hai bảng đấu, mỗi bảng 4 đội. Xác suất để hai đội của Việt Nam nằm ở hai bảng khác nhau bằng
 Giải bởi Vietjack
Giải bởi Vietjack
Chọn D
Nhận định bài toán:
1) Đây là dạng bài toán phân chia một tập hợp ra thành các nhóm có số lượng bằng nhau.
2) Phương pháp:
Dạng bài toán này được phân chia làm 2 loại đó là:
- Các nhóm có thứ tự A, B, C, D…
- Các nhóm không phân biệt thứ tự.
Nếu không phân biệt rõ ràng 2 bài toán này thì rất dễ dẫn đến nhầm lẫn và sai kết quả.
Ví dụ: Có bao nhiêu cách chia 20 người thành 4 nhóm, mỗi nhóm có 5 người trong các trường hợp sau:
a) Các nhóm được đánh tên theo thứ tự A, B, C, D.
b) Không phân biệt thứ tự nhóm.
Lời giải
a) Số cách chọn 5 người cho nhóm A là . Ứng với mỗi cách chọn trên, ta có số cách chọn 5 người cho nhóm B là , nhóm C là và 5 người còn lại vào nhóm D.
Theo quy tắc nhân, ta được số cách chia nhóm là: 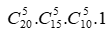 (cách).
(cách).
b) Vì các nhóm không phân biệt thứ tự nên khi ta hoán vị 4 nhóm trên sẽ cho cùng một kết quả. Do đó số cách chia trong trường hợp này là
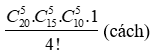
3) Phân tích bài toán và lời giải.
Chia 8 đội thành hai bảng đấu, do đó hai bảng đấu này sẽ có thứ tự rõ ràng cho nên bài toán của chúng ta thuộc loại chia nhóm có thứ tự.
Gọi hai bảng đấu là bảng A và bảng B.
Chọn 4 đội vào bảng A ta có cách, bốn đội còn lại vào bảng B có 1 cách.
Theo quy tắc nhân, ta có số cách chia 8 đội vào hai bảng đấu là:
![]()
Gọi A là biến cố “Hai đội Việt Nam nằm ở hai bảng khác nhau”.
Bảng A: Có 3 đội nước ngoài và 1 đội Việt Nam. Số cách chọn là .
Bảng B: Chỉ còn 1 cách chọn duy nhất cho 3 đội nước ngoài và 1 đội Việt Nam còn lại vào bảng B.
Do đó số cách chia 8 đội thành 2 bảng mỗi bảng có 1 đội Việt Nam là : n(A) = .1 = 40 cách
Vậy xác suất của biến cố A là: 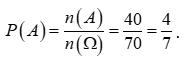
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Có hai dãy ghế đối diện nhau, mỗi dãy có 3 ghế. Xếp ngẫu nhiên 6 học sinh, gồm 3 nam và 3 nữ, ngồi vào hai dãy ghế đó sao cho mỗi ghế có đúng một học sinh ngồi. Xác suất để mỗi học sinh nam đều ngồi đối diện với một học sinh nữ bằng:
Cho tập S = {1;2;3;...;19;20} gồm 20 số tự nhiên từ 1 đến 20. Lấy ngẫu nhiên ba số thuộc S. Xác suất để ba số lấy được lập thành một cấp số cộng là
Gọi A là tập các số tự nhiên có 3 chữ số đôi một khác nhau. Lấy ngẫu nhiên ra từ A hai số. Tính xác suất để lấy được hai số mà các chữ số có mặt ở hai số đó giống nhau.
Cho A là tập tất cả các số tự nhiên có 5 chữ số. Chọn ngẫu nhiên một số từ tập A, tính xác suất để chọn được một số chia hết cho 7 và chữ số hàng đơn vị là chữ số 1.
Cho đa giác 30 đỉnh nội tiếp đường tròn, gọi (S) là tập hợp các đường thẳng đi qua hai trong số 30 đỉnh đã cho. Chọn 2 đường thẳng bất kỳ thuộc tập (S). Tính xác suất để chọn được 2 đường thẳng mà giao điểm của chúng nằm bên trong đường tròn.
Gọi S là tập tất cả các số tự nhiên có 4 chữ số đôi một khác nhau được chọn từ các chữ số 1,2,3,4,5,6,7,8,9. Lấy ngẫu nhiên một số thuộc S. Tính xác suất để lấy được một số chia hết cho 11 và tổng 4 chữ số của nó cũng chia hết cho 11.
Lập một số tự nhiên có 4 chữ số. Tính xác suất để số đó có chữ số đứng trước không nhỏ hơn chữ số đứng sau.
Trong chương trình giao lưu gồm có 15 người ngồi vào 15 ghế theo một hàng ngang. Giả sử người dẫn chương trình chọn ngẫu nhiên 3 người trong 15 người để giao lưu với khán giả. Xác suất để trong 3 người được chọn đó không có 2 người ngồi kề nhau là
Cho tập A = {0;1;2;3;4;5;6}. Xác suất để lập được số tự nhiên gồm 5 chữ số khác nhau lấy từ các phần tử của tập A sao cho số đó chia hết cho 1,2,3 và các chữ số 1,2,3 luôn có mặt cạnh nhau là
Chọn ngẫu nhiên một số tự nhiên có 4 chữ số. Tính xác suất để số được chọn có dạng , trong đó 1abcd9
Gọi X là tập hợp các số tự nhiên có 6 chữ số đôi một khác nhau. Lấy ngẫu nhiên một số thuộc tập X. Xác suất để số lấy được luôn chứa đúng ba số thuộc tập Y = {1;2;3;4;5} và 3 số đứng cạnh nhau, số chẵn đứng giữa hai số lẻ.
Cho tập X = {1;2;3;....;8}. Lập từ X số tự nhiên có 8 chữ số đôi một khác nhau. Xác suất để lập được số chia hết cho 1111 là
Gọi S là tập hợp các số tự nhiên có chín chữ số đôi một khác nhau. Chọn ngẫu nhiên một số thuộc tập S. Xác suất để số được chọn chia hết cho 3 là
Từ tập hợp tất cả các số tự nhiên có năm chữ số mà các chữ số đều khác 0, lấy ngẫu nhiên một số. Xác suất để trong số tự nhiên được lấy ra chỉ có mặt ba chữ số khác nhau là:
Cho một đa giác đều 48 đỉnh. Lấy ngẫu nhiên 3 đỉnh của đa giác. Tính xác suất để tam giác tạo thành từ ba đỉnh đó là một tam giác nhọn.