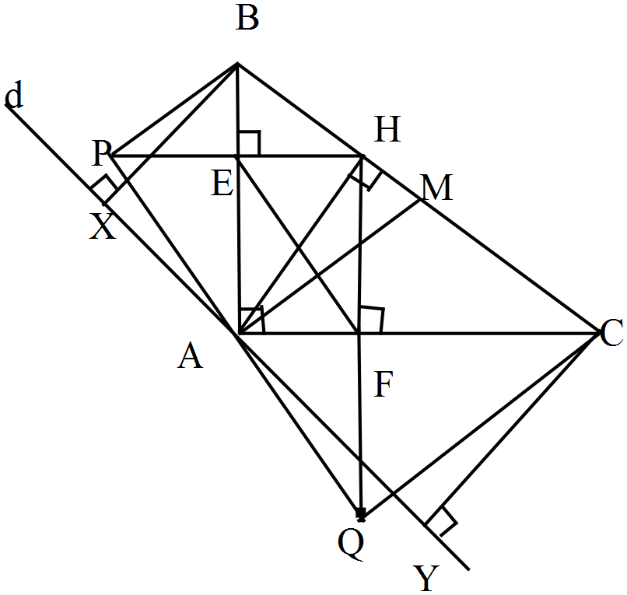
Cho $\Delta ABC$ vuông ở $A,(AB<AC)$, đường cao AH, đường trung tuyến AM. Gọi E, F lần lượt là hình chiếu vuông góc của H trên AB, AC. Trên tia đối của tia EH lấy điểm P sao cho $EP=EH$, trên tia đối của tia FH lấy điểm sao cho $FQ=FH$.
a) Chứng minh ba điểm A, P, Q thẳng hàng.
b) Chứng minh rằng tứ giác BPQC là hình thang vuông và $BP+QC=BC$.
c) Chứng minh AM vuông góc với EF

d) Gọi (d) là đường thẳng thay đổi, đi qua A, nhưng không cắt cạnh BC của tam giác ABC. Gọi X, Y lần lượt là hình chiếu vuông góc của B, C trên (d). Tìm vị trí của (d) để chu vi tứ giác BXYC lớn nhất.

Một chiếc khăn trải bàn có dạng hình chữ nhật ABCD được thêu một hoạ tiết có dạng hình thoi MNPQ ở giữa với MP = x (cm), NQ = y (cm) (x > y > 0) như Hình 5.

Viết đa thức biểu thị diện tích phần còn lại của chiếc khăn trải bàn đó.

Phân tích mỗi đa thức sau thành nhân tử:

a) \(3{x^2} - \sqrt 3 x + \frac{1}{4}\);

b) x² – x – y² + y;

c) x³ + 2x² + x – 16xy².

Tính giá trị của mỗi biểu thức sau:

a) A = 16x² ‒ 8xy + y² ‒ 21 biết 4x = y + 1;

b) B = 25x² + 60xy + 36y² + 22 biết 6y = 2 ‒ 5x;

c) C = 27x³ – 27x²y + 9xy² – y³ – 121 biết 3x = 7 + y.

Thực hiện phép tính:

a) \(7{x^2}{y^5} - \frac{7}{3}{y^2}\left( {3{x^2}{y^3} + 1} \right)\);

b) \(\frac{1}{2}x\left( {{x^2} + {y^2}} \right) - \frac{3}{2}{y^2}\left( {x + 1} \right) - \frac{1}{{\sqrt 4 }}{x^3}\);

c) (x + y)(x2 + y2 + 3xy) ‒ x3 ‒ y3;

d) (‒132xn + 1y10zn + 2 + 143xn + 2y12zn) : (11xny9zn) với n là số tự nhiên.

Cho hai đa thức: M = 23x²³y ‒ 22xy²³ + 21y ‒ 1 và N = ‒22xy³ ‒ 42y ‒ 1.

a) Tính giá trị của mỗi đa thức M, N tại x = 0; y = –2.

b) Tính M + N; M – N.

c) Tìm đa thức P sao cho M – N – P = 63y + 1.

Thực hiện phép tính:

a) \({x^3}\left( { - \frac{5}{4}{x^2}y} \right)\left( {\frac{2}{5}{x^3}{y^4}} \right)\);

b) \(\left( { - \frac{3}{4}{x^5}{y^4}} \right)\left( {x{y^2}} \right)\left( { - \frac{8}{9}{x^2}{y^5}} \right)\).