5 câu hỏi trắc nghiệm thuộc Đề số 8. Top 10 Đề kiểm tra Giữa kì 1 Toán 8 (có đáp án)

$a^{2} + b^{2} + c^{2} = a b + b c + c a \Leftrightarrow 2 a^{2} + 2 b^{2} + 2 c^{2} = 2 a b + 2 b c + 2 c a \Leftrightarrow 2 a^{2} + 2 b^{2} + 2 c^{2} - 2 a b - 2 b c - 2 c a = 0 \Leftrightarrow a^{2} - 2 a b + b^{2} + b^{2} - 2 b c + c^{2} + c^{2} - 2 c a + a^{2} = 0 \Leftrightarrow {(a - b)}^{2} + {(b - c)}^{2} + {(c - a)}^{2} = 0$

Mà ${(a - b)}^{2} \geq 0; {(b - c)}^{2} \geq 0; {(c - a)}^{2} \geq 0$ với mọi số .

Suy ra ${(a - b)}^{2} + {(b - c)}^{2} + {(c - a)}^{2} = 0$
$\Leftrightarrow \{\begin{cases} {(a - b)}^{2} = 0 \\ {(b - c)}^{2} = 0 \\ {(c - a)}^{2} = 0 \end{cases} \Leftrightarrow \{\begin{cases} a - b = 0 \\ b - c = 0 \\ c - a = 0 \end{cases} \Leftrightarrow \{\begin{cases} a = b \\ b = c \\ c = a \end{cases} \Leftrightarrow a = b = c$ (điều phải chứng minh)

Câu 4:

Cho

Δ A B C

vuông ở

A, (A B < A C)

, đường cao AH, đường trung tuyến AM. Gọi E, F lần lượt là hình chiếu vuông góc của H trên AB, AC. Trên tia đối của tia EH lấy điểm P sao cho

E P = E H

, trên tia đối của tia FH lấy điểm sao cho

F Q = F H

.
a) Chứng minh ba điểm A, P, Q thẳng hàng.
b) Chứng minh rằng tứ giác BPQC là hình thang vuông và

B P + Q C = B C

.
c) Chứng minh AM vuông góc với EF

d) Gọi (d) là đường thẳng thay đổi, đi qua A, nhưng không cắt cạnh BC của tam giác ABC. Gọi X, Y lần lượt là hình chiếu vuông góc của B, C trên (d). Tìm vị trí của (d) để chu vi tứ giác BXYC lớn nhất.

Xem đáp án

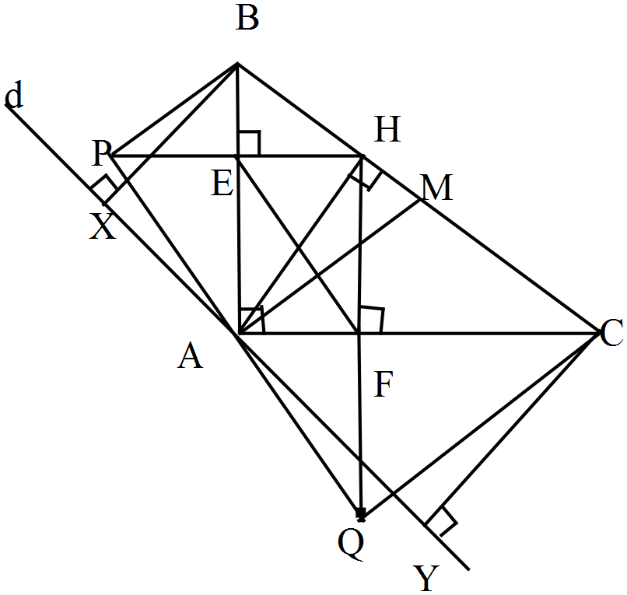
Cho tam giác ABC vuông ở A (AB<AC), đường cao AH, đường trung tuyến (ảnh 1)

a) Ta có P đối xứng với H qua E

\Rightarrow

E là trung điểm của HP
mà AB vuông góc với HP

\Rightarrow

AB là trung trực của HP

\Rightarrow

H đối xứng với P qua AB

\Rightarrow

A P = A H

và góc

\hat{H A E} = \hat{P A E}

Vì Q đối xứng H với qua F

\Rightarrow

F là trung điểm của QH
mà AC vuông góc với QF

\Rightarrow

AC là trung trực của QF

\Rightarrow

H đối xứng với qua Q
và AC

\Rightarrow A Q = A H, \hat{H A F} = \hat{Q A F} \Rightarrow \hat{Q A P} = 2 (\hat{H A E} + \hat{H A F}) = 2 \hat{B A C} = 180^{0}

Ba điểm P, A, Q thẳng hàng.
b) Xét

Δ A Q C

và

Δ A H C

có

A Q = A H

(cmt)

\hat{H A F} = \hat{Q A F}

(cmt)
AC chung

\Rightarrow Δ A Q C = Δ A H C

= (c.g.c)

\Rightarrow C Q = C H; \hat{C Q A} = \hat{C H A} = 90_{}^{0}

Chứng minh tương tự ta có :

B P = B H; \hat{B P A} = \hat{B H A} = 90_{}^{0} \Rightarrow B P + Q C = B H + C H = B C

Xét tứ giác có BPQ có

B P ⊥ P Q; C Q ⊥ P Q \Rightarrow B P // C Q

Mà

\hat{C Q A} = 90_{}^{0}

\Rightarrow B P Q C

là hình thang vuông.
c) Xét tam giác QHP có EF là đường trung bình suy ra EF//PQ
Ta có :

A H = A Q (Δ A Q C = Δ A H C) A H = A P (Δ A P B = Δ A H B) \Rightarrow A P = A Q

Mà

B M = M C

Hình thang BCQP có AM là đường trung bình suy ra AM//CQ

P Q ⊥ C Q \Rightarrow P Q ⊥ A M \Rightarrow E F ⊥ A M

d) Ta có:

{(B X + A X)}^{2} \leq 2 (B X^{2} + A X^{2}) = 2 A B^{2}

\Rightarrow B X + A X \leq A B \sqrt{2} {(C Y + A Y)}^{2} \leq 2 (C Y^{2} + A Y^{2}) = 2 A C^{2} \Rightarrow C Y + A Y \leq A C \sqrt{2}

Chu vi hình thang

P_{B X Y C}

= B X + X Y + C Y + B C = B X + A X + A Y + C Y + B C \leq A B \sqrt{2} + A C \sqrt{2} + B C

P_{B X Y C} \max = A B \sqrt{2} + A C \sqrt{2} + B C

\Leftrightarrow

d là phân giác góc ngoài tại đỉnh A hay d vuông góc với phân giác .

Câu 5:

a) ( Dành cho các lớp 8B, 8C, 8D, 8E )
Cho a, b, c là các số thực đôi một khác nhau thỏa mãn

a^{3} + b^{3} + c^{3} = 3 a b c

. Tính giá trị của biểu thức

M = (a + b) (b + c) (c + a) + a b c

b) ( Dành riêng cho lớp 8A)
Với a, b là các số thực thỏa mãn

a^{3} + b^{3} - 3 a b = - 18

.
Chứng minh rằng

- 9 < a + b < - 1

Xem đáp án

a) Ta có:

a^{3} + b^{3} + c^{3} = 3 a b c \Rightarrow (a^{3} + b^{3}) + c^{3} - 3 a b c = 0 \Rightarrow a^{3} + 3 a^{2} b + 3 a b^{2} + b^{3} + c^{3} - 3 a b c - 3 a^{2} b - 3 a b^{2} = 0 \Rightarrow {(a + b)}^{3} + c^{3} - 3 a b (a + b + c) = 0 \Rightarrow (a + b + c) [{(a + b)}^{2} - (a + b) c + c^{2}] - 3 a b (a + b + c) = 0 \Rightarrow (a + b + c) [a^{2} + 2 a b + b^{2} - a c - b c + c^{2} - 3 a b] = 0 \Rightarrow (a + b + c) (a^{2} + b^{2} + c^{2} - a b - a c - b c) = 0 \Rightarrow \frac{1}{2} (a + b + c) [{(a - b)}^{2} + {(b - c)}^{2} + {(c - a)}^{2}] = 0 \Rightarrow [\begin{array}{l} a + b + c = 0 \\ a = b = c \end{array} T H 1 : a + b + c = 0 \Rightarrow a + b = - c; b + c = - a; c + a = - b

Khi đó

M = (- c) (- a) (- b) + a b c = - a b c + a b c = 0

TH2:

a = b = c

\Rightarrow M = 2 a .2 b .2 c + a b c = 8 a b c + a b c = 9 a b c

b) Ta có

a^{3} + b^{3} - 3 a b = - 18 \Rightarrow a^{3} + b^{3} + 1 - 3 a b = - 17 \Rightarrow {(a + b)}^{3} - 3 a b (a + b) + 1 - 3 a b = - 17 \Rightarrow (a + b + 1) [{(a + b)}^{2} - (a + b) + 1] - 3 a b (a + b + 1) = - 17 \Rightarrow (a + b + 1) (a^{2} + b^{2} + 1 - a b - a - b) = - 17 < 0 \Rightarrow (a + b + 1) (a^{2} + b^{2} + 1 - a b - a - b) < 0

mà

a^{2} + b^{2} + 1 - a b - a - b = \frac{1}{2} [{(a - b)}^{2} + {(a - 1)}^{2} + {(b - 1)}^{2}] > 0

ra vì theo giả thiết không thể đồng thời bằng)

\Rightarrow a + b + 1 < 0 \Rightarrow a + b < - 1

Ta có:

{(a + b)}^{3} - 3 a b (a + b + 1) = - 18 {(a - b)}^{2} \geq 0 \Rightarrow 3 a b \leq \frac{3}{4} {(a + b)}^{2} \Rightarrow 3 a b (a + b + 1) \geq \frac{3}{4} {(a + b)}^{2} (a + b + 1)

(vì

a + b + 1 < 0

)

Đặt

a + b = t \Rightarrow - 18 \leq t^{3} - \frac{3}{4} t^{2} (t + 1) \Rightarrow \frac{1}{4} t^{3} - \frac{3}{4} t^{2} + 18 \geq 0 \Rightarrow \frac{1}{4} (t^{3} - 3 t^{2} + 72) \geq 0 \Rightarrow t^{3} - 3 t^{2} + 72 \geq 0 \Rightarrow t^{3} \geq - 72 + 3 t^{2} \geq - 72 \Rightarrow t^{3} \geq - 72 \Rightarrow t > - 5 > - 9 \Rightarrow a + b > - 9

Vậy

- 9 < a + b < - 1

CHỌN BỘ SÁCH BẠN MUỐN XEM

Top 10 Đề kiểm tra Giữa kì 1 Toán 8 (có đáp án)

Đề số 8. Top 10 Đề kiểm tra Giữa kì 1 Toán 8 (có đáp án)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương