Khi nhân hai lũy thừa cùng cơ số: . Kết quả là:
A. ;
B. ;
C. ;
D. .
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án B
Ta có: .
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Truyền thuyết Ấn Độ kể rằng người phát minh ra bàn cờ vua đã chọn phần thưởng là số thóc rải trên 64 ô của bàn cờ vua như sau: ô thứ nhất để 1 hạt thóc, ô thứ hai để 2 hạt thóc, ô thứ ba để 4 hạt thóc, ô thứ tư để 8 hạt thóc,… Cứ như thế số hạt ở ô sau gấp đôi số hạt ở ô trước. Hỏi ô số 34 của bàn cờ có bao nhiêu hạt thóc.
Theo các nhà khoa học, mỗi giây cơ thể con người trung bình tạo ra khoảng 25. tế bào hồng cầu (theo www.healthline.com). Hãy tính xem mỗi giờ, bao nhiêu tế bào hồng cầu được tạo ra?
a) Viết kết quả phép nhân sau dưới dạng một lũy thừa của 7:
= (7 . 7) . (7 . 7 . 7) = ?
b) Nêu nhận xét về mối liên hệ giữa các số mũ của 7 trong hai thừa số và trong tích tìm được ở câu a).
Truyền thuyết Ấn Độ kể rằng, người phát minh ra bàn cờ vua đã chọn phần thưởng là số thóc rải trên 64 ô của bàn cờ vua như sau: ô thứ nhất để 1 hạt thóc, ô thứ hai để 2 hạt, ô thứ ba để 4 hạt, ô thứ tư để 8 hạt, …Cứ như thế, số hạt ở ô sau gấp đôi số hạt ở ô trước. Liệu nhà vua có đủ thóc để thưởng cho nhà phát minh đó hay không?
Khối lượng của trái đất khoảng 6. tấn. Khối lượng mặt trăng khoảng 7,4. tấn. Hỏi khối lượng trái đất gấp bao nhiêu lần khối lượng mặt trăng.
+ Lũy thừa bậc n của số tự nhiên a là tích của n thừa số bằng nhau, mỗi thừa số bằng a:
an = 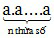 (n ∈ N*)
(n ∈ N*)
an đọc là “a mũ n” hoặc “ a lũy thừa n”, a là cơ số, n là số mũ.
Chú ý: Ta có a1 = a.
a2 cũng được gọi là a bình phương (hay bình phương của a);
a3 cũng được gọi là a lập phương (hay lập phương của a).
Ví dụ 1. Viết các biểu thức sau dưới dạng lũy thừa:
a) 4.4.4.4.4.4.4;
b) 11.11.11;
c) 8.8.8.8.8.
Lời giải
a) 4.4.4.4.4.4.4 = 47;
b) 11.11.11 = 113;
c) 8.8.8.8.8 = 85.
+ Nhân hai lũy thừa cùng cơ số, ta giữ nguyên cơ số và công các số mũ:
am.an = am+n.
Ví dụ 2. Viết kết quả của các phép tính sau dưới dạng một lũy thừa:
a) a2.a3.a5;
b) 23.28.27;
c) 7.72.723.
Lời giải
a) a2.a3.a5 = a2 + 3 + 5 = a10;
b) 23.28.27 = 23 + 8 + 7 = 218;
c) 7.72.723 = 71 + 2 + 23 = 726.
Chia hai lũy thừa cùng cơ số, ta giữ nguyên cơ số và trừ các số mũ:
am:an = am-n.
Ví dụ 3. Viết kết quả của phép tính dưới dạng một lũy thừa:
a) 1212:12;
b) 108:105:103.
Lời giải
a) 1212:12 = 1212 – 1 = 1211;
b) 108:105:103 = 108 – 5 : 103 = 103 : 103 = 103 – 3 = 100 = 1.
B. Bài tập
Bài 1. Hoàn thành bảng sau:
|
Lũy thừa |
Cơ số |
Số mũ |
Giá trị của biểu thức |
|
52 |
|
|
|
|
|
6 |
3 |
|
|
25 |
|
|
|
|
|
10 |
|
1000 |
Lời giải
|
Lũy thừa |
Cơ số |
Số mũ |
Giá trị của biểu thức |
|
52 |
5 |
2 |
25 |
|
63 |
6 |
3 |
216 |
|
25 |
2 |
5 |
32 |
|
103 |
10 |
3 |
1000 |
Bài 2. Khối lượng của trái đất khoảng 6.1021 tấn. Khối lượng mặt trăng khoảng 7,4.1019 tấn. Hỏi khối lượng trái đất gấp bao nhiêu lần khối lượng mặt trăng.
Lời giải
Khối lượng trái đất gấp số lần khối lượng mặt trăng là:
6.1021 : (7,4.1019) = 600.1019:(7,4.1019) = (600:7,4) ≈ 81 (lần).
Khối lượng trái đất gấp 81 lần khối lượng mặt trăng.