Cho hàm số $y = \frac{1}{3}{x^3} - \frac{1}{2}\left( {m + 3} \right){x^2} + {m^2}x + 1.$ Có bao nhiêu số thực $m$ để hàm số đạt cực trị tại $x = 1?$

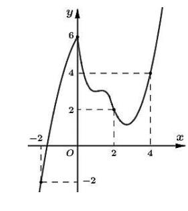
Cho hàm số $y = f\left( x \right)$ có đồ thị như hình vẽ.

Trong đoạn $\left[ { - 20;20} \right]$, có bao nhiêu số nguyên $m$ để hàm số $y = \left| {10f\left( {x - m} \right) - \frac{{11}}{3}{m^2} + \frac{{37}}{3}m} \right|$ có 3 điểm cực trị?

Cho hàm số $f\left( x \right).$ Hàm số $y = f'\left( x \right)$ có đồ thị như hình bên dưới.

Hàm số $g\left( x \right) = f\left( {3 - 4x} \right) - 8{x^2} + 12x + 2020$ nghịch biến trên khoảng nào dưới đây?

Cho hình hộp $ABCD.A'B'C'D'$ có đáy là hình chữ nhật, $AB = \sqrt 3 ,AD = \sqrt 7 .$ Hai mặt bên $\left( {ABB'A'} \right)$ và $\left( {ADD'A'} \right)$ lần lượt tạo với đáy góc ${45^0}$ và ${60^0},$ biết cạnh bên bằng 1. Tính thể tích khối hộp.

Cho biết đồ thị hàm số $y = {x^4} - 2m{x^2} - 2{m^2} + {m^4}$ có 3 điểm cực trị $A,B,C$ cùng với điểm $D\left( {0; - 3} \right)$ là 4 đỉnh của một hình thoi. Gọi $S$ là tổng các giá trị $m$ thỏa mãn đề bài thì $S$ thuộc khoảng nào sau đây

Một vật có phương trình chuyển động $S\left( t \right) = 4,9{t^2};$ trong đó t tính bằng (s), S(t) tính bắng mét (m). Vận tốc của vật tại thời điểm t=6s bằng

Tìm số hạng không chứa $x$ trong khai triển ${\left( {x - \frac{2}{x}} \right)^n},n \in {\mathbb{N}^*}$ biết $C_n^1 - 2.2.C_n^2 + {3.2^2}.C_n^3 - {4.2^3}.C_n^4 + {5.2^4}C_n^5 + ... + {\left( { - 1} \right)^n}.n{.2^{n - 1}}C_n^n = - 2022$

Đồ thị hàm số $y = \frac{{{x^2} - 3x + 2}}{{{x^3} - x}}$ có mấy đường tiệm cận?

Hàm số $y = \sqrt {2x - {x^2}}$ nghịch biến trên khoảng:

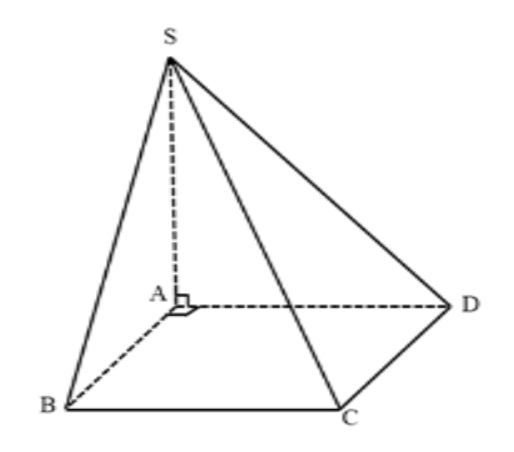
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật, $AB = a,AD = a\sqrt 2 ,$ đường thẳng $SA$ vuông góc với $mp\left( {ABCD} \right).$ Góc giữa $SC$ và $mp\left( {ABCD} \right)$ bằng ${60^0}.$ Tính thể tích khối chóp $S.ABCD$

Xét phép thử T: “Gieo một con súc sắc cân đối và đồng chất” và biến cố A liên quan đến phép thử: “Mặt lẻ chấm xuất hiện”. Chọn khẳng định sai trong những khẳng định dưới đây:

Cho tứ diện đều $ABCD$ có cạnh bằng 1, gọi $M$ là trung điểm $AD$ và $N$ trên cạnh $BC$ sao cho $BN = 2NC.$ Khoảng cách giữa hai đường thẳng $MN$ và $CD$ là

Đồ thị hàm số $y = \frac{{x - 2}}{{x + 4}}$ cắt trục tung tại điểm có tung độ bằng

Mệnh đề nào sau đây sai:

Cho hình chóp tứ giác $S.ABCD$ có $SA = x$ và tất cả các cạnh còn lại đều bằng 1. Khi thể tích khối chóp $S.ABCD$ đạt giá trị lớn nhất thì $x$ nhận giá trị nào sau đây?

Trong các phương trình dưới đây, phương trình nào có tập nghiệm là: $x = \frac{\pi }{2} + k\pi ,k \in \mathbb{Z}.$