Cho hình chóp tứ giác \(S.ABCD\) có \(SA = x\) và tất cả các cạnh còn lại đều bằng 1. Khi thể tích khối chóp \(S.ABCD\) đạt giá trị lớn nhất thì \(x\) nhận giá trị nào sau đây?
A.\(x = \frac{{\sqrt {35} }}{7}\)
B.\(x = 1.\)
C.\(x = \frac{9}{4}\)
D. \(x = \frac{{\sqrt {34} }}{7}\)
 Giải bởi Vietjack
Giải bởi Vietjack
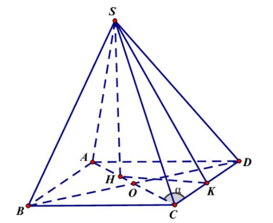
Gọi
\(H\)là tâm đường tròn ngoại tiếp tam giác \(BCD,\) do \(SB = SC = SD\) nên \(SH\) là trục của đường tròn ngoại tiếp tam giác \(BCD,\) suy ra \(SH \bot \left( {ABCD} \right).\)
Do tứ giác \(ABCD\) là hình thoi nên \(AC\) là đường trung trực của đường thẳng \(BD\) do đó \(H \in AC.\)
Đặt \(\alpha = \widehat {ACD},0 < \alpha < \frac{\pi }{2} \Rightarrow \widehat {BCD} = 2\alpha ,\) suy ra \({S_{ABCD}} = 2{S_{BCD}} = BC.CD.\sin \widehat {BCD} = \sin 2\alpha .\)
Gọi \(K\) là trung điểm của \(CD \Rightarrow CD \bot SK,\) mà \(CD \bot SH\) suy ra \(CD \bot HK.\)
\(HC = \frac{{CK}}{{\cos \alpha }} = \frac{1}{{2\cos \alpha }},SH = \sqrt {S{C^2} - H{C^2}} = \sqrt {1 - \frac{1}{{4{{\cos }^2}\alpha }}} = \frac{{\sqrt {4{{\cos }^2}\alpha - 1} }}{{2\cos \alpha }}\).
Thể tích khối chóp \(S.ABCD\) là \(V = \frac{1}{3}SH.{S_{ABCD}} = \frac{1}{3}\frac{{\sqrt {4\cos \alpha - 1} }}{{2\cos \alpha }}.\sin 2\alpha = \frac{1}{3}\sin \alpha \sqrt {4{{\cos }^2}\alpha - 1} \)
Do đó \(V = \frac{1}{6}\left( {2\sin \alpha } \right)\sqrt {4{{\cos }^2}\alpha - 1} \le \frac{1}{6}\frac{{4{{\sin }^2}\alpha + 4{{\cos }^2}\alpha - 1}}{2} = \frac{1}{4}.\)
Dấu “=” xảy ra khi \(2\sin \alpha = \sqrt {4{{\cos }^2}\alpha - 1} \Leftrightarrow 4{\sin ^2}\alpha = 4{\cos ^2}\alpha - 1 \Leftrightarrow {\cos ^2}\alpha = \frac{5}{8}\)
\( \Leftrightarrow \cos \alpha = \frac{{\sqrt {10} }}{4}.\) Khi đó \(HC = \frac{2}{{\sqrt {10} }},SH = \frac{{\sqrt {15} }}{5}.\)
Gọi \(O = AC \cap BD,\) suy ra \(AC = 2OC = 2CD.\cos \alpha = \frac{{\sqrt {10} }}{2}.\)
\(AH = AC - HC = \frac{{\sqrt {10} }}{2} - \frac{2}{{\sqrt {10} }} = \frac{3}{{\sqrt {10} }}.\)
Vậy \(x = SA = \sqrt {S{H^2} + A{H^2}} = \sqrt {\frac{3}{5} + \frac{9}{{10}}} = \frac{{\sqrt 6 }}{2}.\)
Đáp án D.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ.
![Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ. Trong đoạn \(\left[ { - 20;20} \right]\), có bao nhiêu số nguyên \(m\) để hàm số \(y = \left| {10f\left( {x - m} \right) - \frac{{ (ảnh 1)](https://video.vietjack.com/upload2/images/1649521444/1649521622-image30.png)
Trong đoạn \(\left[ { - 20;20} \right]\), có bao nhiêu số nguyên \(m\) để hàm số \(y = \left| {10f\left( {x - m} \right) - \frac{{11}}{3}{m^2} + \frac{{37}}{3}m} \right|\) có 3 điểm cực trị?
Cho hàm số \(f\left( x \right).\) Hàm số \(y = f'\left( x \right)\) có đồ thị như hình bên dưới.
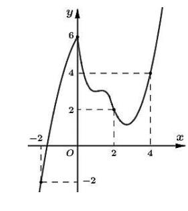
Hàm số \(g\left( x \right) = f\left( {3 - 4x} \right) - 8{x^2} + 12x + 2020\) nghịch biến trên khoảng nào dưới đây?
Cho hình hộp \(ABCD.A'B'C'D'\) có đáy là hình chữ nhật, \(AB = \sqrt 3 ,AD = \sqrt 7 .\) Hai mặt bên \(\left( {ABB'A'} \right)\) và \(\left( {ADD'A'} \right)\) lần lượt tạo với đáy góc \({45^0}\) và \({60^0},\) biết cạnh bên bằng 1. Tính thể tích khối hộp.
Cho biết đồ thị hàm số \(y = {x^4} - 2m{x^2} - 2{m^2} + {m^4}\) có 3 điểm cực trị \(A,B,C\) cùng với điểm \(D\left( {0; - 3} \right)\) là 4 đỉnh của một hình thoi. Gọi \(S\) là tổng các giá trị \(m\) thỏa mãn đề bài thì \(S\) thuộc khoảng nào sau đây
Một vật có phương trình chuyển động \(S\left( t \right) = 4,9{t^2};\) trong đó t tính bằng (s), S(t) tính bắng mét (m). Vận tốc của vật tại thời điểm t=6s bằng
Tìm số hạng không chứa \(x\) trong khai triển \({\left( {x - \frac{2}{x}} \right)^n},n \in {\mathbb{N}^*}\) biết \(C_n^1 - 2.2.C_n^2 + {3.2^2}.C_n^3 - {4.2^3}.C_n^4 + {5.2^4}C_n^5 + ... + {\left( { - 1} \right)^n}.n{.2^{n - 1}}C_n^n = - 2022\)
Đồ thị hàm số \(y = \frac{{{x^2} - 3x + 2}}{{{x^3} - x}}\) có mấy đường tiệm cận?
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình chữ nhật, \(AB = a,AD = a\sqrt 2 ,\) đường thẳng \(SA\) vuông góc với \(mp\left( {ABCD} \right).\) Góc giữa \(SC\) và \(mp\left( {ABCD} \right)\) bằng \({60^0}.\) Tính thể tích khối chóp \(S.ABCD\)
Cho tứ diện đều \(ABCD\) có cạnh bằng 1, gọi \(M\) là trung điểm \(AD\) và \(N\) trên cạnh \(BC\) sao cho \(BN = 2NC.\) Khoảng cách giữa hai đường thẳng \(MN\) và \(CD\) là
Xét phép thử T: “Gieo một con súc sắc cân đối và đồng chất” và biến cố A liên quan đến phép thử: “Mặt lẻ chấm xuất hiện”. Chọn khẳng định sai trong những khẳng định dưới đây:
Đồ thị hàm số \(y = \frac{{x - 2}}{{x + 4}}\) cắt trục tung tại điểm có tung độ bằng
Trong các phương trình dưới đây, phương trình nào có tập nghiệm là: \(x = \frac{\pi }{2} + k\pi ,k \in \mathbb{Z}.\)
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình bên dưới.
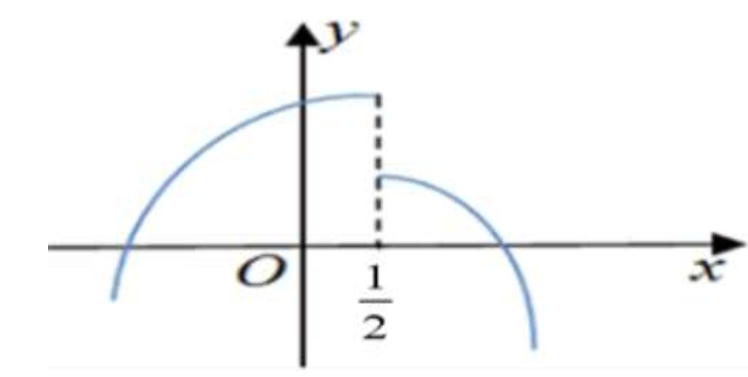
Khi đó