Hàm số y=|(x−1)3(x+1)| có bao nhiêu điểm cực trị?
A.2.
B.4.
C.3.
D.1.
 Giải bởi Vietjack
Giải bởi Vietjack
f(x)=(x−1)3(x+1).
f′(x)=3(x−1)2(x+1)+(x−1)3=(x−1)2(4x+2).
f′(x)=0⇔(x−1)2(4x+2)=0⇔[x=1⇒y=0x=−12⇒y=−2716.
f′(−1)=0.
Bảng biến thiên:
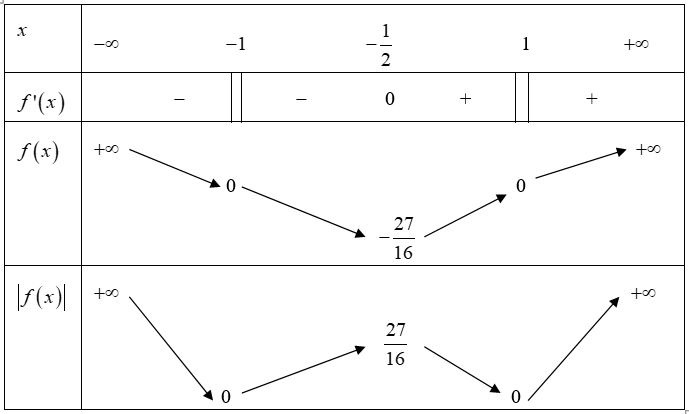
Dựa vào bảng biến thiên ta thấy hàm số y=|(x−1)3(x+1)| có 3 cực trị.
Đáp án C
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho hàm đa thức y=f(x). Hàm số y=f′(x) có đồ thị như hình vẽ sau
![Cho hàm đa thức \(y = f(x)\). Hàm số \(y = f'(x)\) có đồ thị như hình vẽ sau Có bao nhiêu giá trị của \(m \in \left[ {0;\,6} \right];\,2m \in \mathbb{Z}\) để hàm số \(g(x) = f\left( {{x^2} - (ảnh 1)](https://video.vietjack.com/upload2/images/1649615523/1649615702-image19.png)
Có bao nhiêu giá trị của m∈[0;6];2m∈Z để hàm số g(x)=f(x2−2|x−1|−2x+m) có đúng 9 điểm cực trị?
Cho hình chóp S.ABCD, đáy là hình chữ nhật tâm O, AB=a, AD=a√3, SA=3a, SO vuông góc với mặt đáy (ABCD). Thể tích khối chóp bằng
Số giá trị nguyên của tham số m để hàm số y=mx4−(m−3)x2+m2không có điểm cực đại là
Cho hàm số y=x+mx−1 có đồ thị là đường cong (H) và đường thẳng Δ có phương trình y=x+1. Số giá trị nguyên của tham số m nhỏ hơn 10 để đường thẳng Δ cắt đường cong (H) tại hai điểm phân biệt nằm về hai nhánh của đồ thị.
Tính tổng tất cả các nghiệm của phương trình sau 32x+8−4.3x+5+27=0.
Cho hàm số y=f(x) có đạo hàm f'. Giá trị nhỏ nhất của hàm số trên \left( {0; + \infty } \right) là
Cho hàm số y = {x^3} - 6{x^2} + 7x + 5 có đồ thị là \left( C \right). Phương trình tiếp tuyến của \left( C \right) tại điểm có hoành độ bằng 2 là:
Cho x,y là các số thực thỏa mãn {\log _9}x = {\log _{12}}y = {\log _{16}}\left( {x + 2y} \right). Giá trị tỉ số \frac{x}{y} là
Cho hàm số y = f(x) liên tục trên \mathbb{R} và có bảng biến thiên
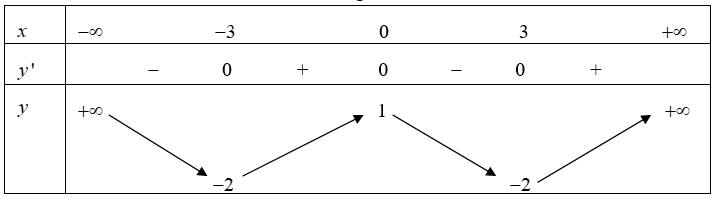
Tìm m để phương trình 2f(x) + m = 0 có đúng 3 nghiệm phân biệt
Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông tại A. Biết AB = AA' = a, AC = 2a. Gọi M là trung điểm của AC. Diện tích mặt cầu ngoại tiếp tứ diện MA'B'C' bằng
Cho hàm số y = \left( {x + 1} \right)\left( {2x + 1} \right)\left( {3x + 1} \right)\left( {m + \left| {2x} \right|} \right) và y = - 12{x^4} - 22{x^3} - {x^2} + 10x + 3 có đồ thị lần lượt là \left( {{C_1}} \right) và \left( {{C_2}} \right) . có bao nhiêu giá trị nguyên của tham số m trên đoạn \left[ { - 2020;2020} \right] để \left( {{C_1}} \right) cắt \left( {{C_2}} \right) tại 3 điểm phân biệt.
Cho hình chóp S.ABCD có đáy là hình vuông, cạnh bên SA vuông góc với đáy. Gọi M, N là trung điểm của SA, SB. Mặt phẳng MNCD chia hình chóp đã cho thành hai phần. tỉ số thể tích hai phần S.MNCD và MNABCD là
Cho hàm số f(x) = - \frac{1}{3}{x^3} + m{x^2} + \left( {3m + 2} \right)x - 5 . Tập hợp các giá trị của tham số m để hàm số nghịch biến trên \mathbb{R} là \left[ {a;\,b} \right]. Khi đó 2a - b bằng