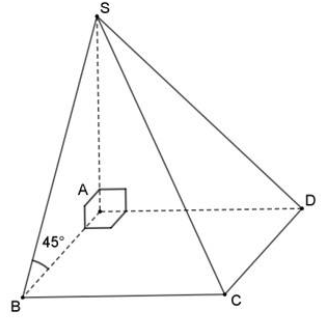
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình chữ nhật, \(SA\) vuông góc với đáy, \(AB = a,AD = 2a.\) Góc giữa \(SB\) và đáy bằng \({45^0}.\) Thể tích của khối chóp \(S.ABCD\) bằng

Có bao nhiêu giá trị nguyên của tham số \(m \in \left( {0;20} \right]\) để hàm số \(y = \frac{{x + 2}}{{x + 3m}}\) đồng biến trên khoảng \(\left( { - \infty ; - 6} \right)?\) 

Đồ thị của hàm số \[y = {x^3} - 3{x^2} - 9x + 1\] có hai điểm cực trị là \(A\) và \(B.\) Điểm nào dưới đây thuộc đường thẳng \(AB?\) 

Gọi \(S\) là tập hợp các số tự nhiên có 6 chữ số được lập từ tập hợp \(A = \left\{ {0;1;2;...;9} \right\}.\) Chọn ngẫu nhiên một số từ tập \(S.\) Tính xác suất để chọn được số tự nhiên có tích các chữ số là 1400. 

Gọi \(m\) là tham số thực để giá trị lớn nhất của hàm số \(y = \left| {{x^2} + 2x + m - 4} \right|\) trên đoạn \(\left[ { - 2;1} \right]\) đạt giá trị nhỏ nhất. Giá trị của \(m\) là 

Có bao nhiêu giá trị nguyên của tham số \(m\) để phương trình \(\left| {\sin x - \cos x} \right| + 4\sin 2x = m\) có nghiệm thực? 

Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:

Biết \(f\left( 0 \right) = 0,\) số nghiệm thuộc đoạn \(\left[ { - \frac{\pi }{6};\frac{{7\pi }}{3}} \right]\) của phương trình \(f\left( {f\left( {\sqrt 3 \sin x + \cos x} \right)} \right) = 1\) là

Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f'\left( x \right) = {\left( {x - 3} \right)^{2020}}\left( {{\pi ^{2x}} - {\pi ^x} + 2021} \right)\left( {{x^2} - 2x} \right),\forall x \in \mathbb{R}.\) Gọi \(S\) là tập các giá trị nguyên của tham số \(m\) để hàm số \(y = f\left( {{x^2} - 8x + m} \right)\) có đúng ba điểm cực trị \({x_1},{x_2},{x_3}\) thỏa mãn \(x_1^2 + x_2^2 + x_3^2 = 50.\) Khi đó tổng các phần tử của \(S\) bằng  

Tiệm cận ngang của đồ thị hàm số \(y = \frac{{3x - 1}}{{1 - x}}\) là 

Cho hàm số \(y = \frac{1}{3}{x^3} - m{x^2} + \left( {{m^2} - m - 1} \right)x + 1.\) Có bao nhiêu giá trị nguyên của tham số thực \(m\) để hàm số đạt cực trị tại \({x_1},{x_2}\) thỏa mãn \(x_1^2 + 2m{x_2} - 3{m^2} + m - 5 \le 0?\)

Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ sau

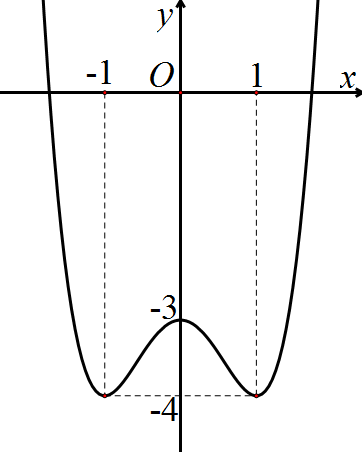
Tất cả các giá trị của tham số thực \(m\) để phương trình \(f\left( x \right) = m\) có 4 nghiệm phân biệt là

Từ các chữ số 1, 2, 3, 4 lập được bao nhiêu số tự nhiên có 3 chữ số? 

Số đỉnh của một khối lăng trụ tam giác là 

Cho cấp số nhân \(\left( {{u_n}} \right)\) với \({u_1} = 2\) và \({u_2} = 8.\) Công bội của cấp số nhân đã cho bằng

Cho hàm số \(y = f\left( x \right)\) xác định, liên tục trên \(\mathbb{R}\) và có bảng biến thiên sau:

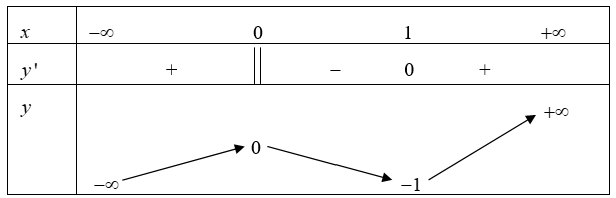
 Khẳng định nào sau đây là khẳng định đúng?