Ông An muốn xây một bể nước chứa dạng hình hộp chữ nhật, phần nắp trên ông để trống một ô có diện tích bằng 20% diện tích của đáy bể. Biết đáy bể là một hình chữ nhật có chiều dài gấp đôi chiều rộng, bể có thể chứa tối đa $10m^3$ nước và giá tiền thuê nhân công là 500000 đồng/ $m^3$. Số tiền ít nhất mà ông phải trả cho nhân công gần nhất với đáp án nào dưới đây?

Cho hàm số y=f(x) có bảng biến thiên như sau:

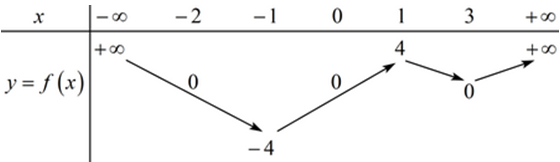
Hàm số $g\left(x\right)=\frac{1}{f\left(x\right)}$ đồng biến trên khoảng nào dưới đây?

Tập xác định của hàm số $y={\left(x^3-27\right)}^{\frac{\pi }{3}}$ là

Cho hình chóp S.ABCD có SA vuông góc với mặt phẳng (ABCD), $SA=a\sqrt{2}$, ABCD là hình vuông tâm O cạnh 2a. Góc giữa hai mặt phẳng (SBD) và (ABCD) bằng

Một nhóm học sinh có 8 học sinh nữ và 4 học sinh nam. Xếp ngẫu nhiên nhóm học sinh này thành một hàng dọc. Tính xác suất sao cho không có hai bạn nam nào đứng cạnh nhau

Cho hàm số $y=x^3-3x^2+mx+1$ có đồ thị hàm số (C) và đường thẳng $d:y=2x+1$. Có bao nhiêu giá trị nguyên dương của tham số m để (C) cắt đường thẳng d tại 3 điểm phân biệt?

Tập nghiệm của bất phương trình ${\log }_{\frac{1}{3}}\frac{1-2x}{x}>0$ có dạng (a,b). Tính T=3a-2b  

Cho hình lập phương ABCD.A'B'C'D' cạnh a. Gọi M là trung điểm cạnh C'D', G là trọng tâm tam giác ABD. Tính khoảng cách từ C đến mặt phẳng $\left(B^{\text{'}}MG\right)$. 

Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 2a, cạnh bên bằng $a\sqrt{3}$. Tính thể tích Vcủa khối cầu ngoại tiếp hình chóp S.ABCD

Tính tổng T tất cả các nghiệm của phương trình ${4.9}^x-{13.6}^x+{9.4}^x=0.$

Khối lăng trụ có chiều cao bằng h, diện tích đáy bằng B có thể tích là

Cho hình nón (N) đỉnh S có bán kính đáy bằng a và diện tích xung quanh $S_{xq}=2\pi a^2$. Tính thể tích V của khối chóp tứ giác đều S.ABCD có đáy ABCD nội tiếp đáy của khối nón (N). 

Hàm số nào dưới đây có nhiều cực trị nhất?

Cho hàm số đa thức bậc năm y=f(x) có đồ thị như hình bên dưới:

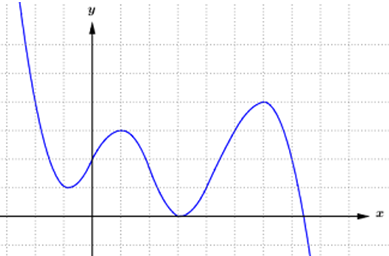
Số nghiệm của phương trình $f\left(xf\left(x\right)\right)=\sqrt{9-x^2{f}^2\left(x\right)}$ là

Cho hàm số f(x) có bảng biến thiên như sau:

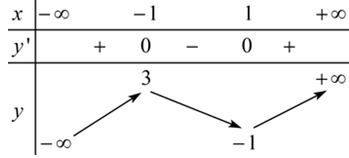
Mệnh đề nào dưới đây sai?

Hàm số nào sau đây có đồ thị phù hợp với hình vẽ?