Cho hình chóp S.ABC có , Mlà điểm bất kì trong không gian. Gọi d là tổng các khoảng cách từ M đến tất cả các đường thẳng AB, BC, CA, SA, SB, SC. Giá trị nhỏ nhất của d bằng:
A. .
B. .
C. .
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án C
Gọi E và F là trung điểm của BC và AB và O là trọng tâm tam giác ABC ta có:
Do . Dựng suy ra EK là đoạn vuông góc cung của SA và BC. Tương tự dựng FI; RL là các đoạn vuông góc chung của 2 cạnh đối diện.
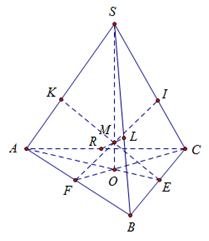
Do tính chất đối xứng ta dễ dàng suy ra EK, FI, RL đồng quy tại điểm M
Như vậy
Mặc khác
Do đó:
Do vậy
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho hình chóp đều S.ABC có cạnh đáy bằng a, cạnh bên bằng 3a. Thể tích khối chóp S.ABC tính theo a là:
Có bao nhiêu số nguyên m để phương trình có hai nghiệm thỏa mãn ?
Cho hình lăng trụ ABC.A'B'C' có độ dài tất cả các cạnh bằng a và hình chiếu vuông góc của đỉnh C lên mặt phẳng (ABB'A') là tâm của hình bình hành ABB'A'. Thể tích khối lăng trụ ABC.A'B'C' tính theo a là:
Cho hàm số . Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số cắt trục hoành tại ba điểm phân biệt.