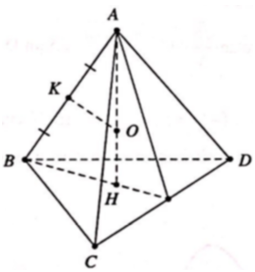
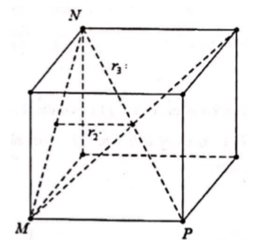
Cho tứ diện đều ABCD có mặt cẩu nội tiếp là (S₁) và mặt cầu ngoại tiếp là (S₂). Một hình lập phương ngoại tiếp (S₂) và nội tiếp trong mặt cầu (S₃). Gọi ${\mathrm{r}}_1,{\mathrm{r}}_2,{\mathrm{r}}_3$ lần lượt là bán kính các mặt cầu (S₁), (S₂), (S₃). Khẳng định nào sau đây là đúng

Cho hình chóp S.ABCD có đáy ABCD là nửa lục giác đều nội tiếp đường tròn đường kính AB = 2a. $\mathrm{SA}\perp$(ABCD) và SA=$\mathrm{a}\sqrt{3}$. Côsin của góc tạo bới hai mặt phẳng (SBC) và (SCD) bằng

Cho hình chóp S.ABC có SA$\perp$(ABC) tam giác ABC đều cạnh a và SA = a (tham khảo hình vẽ bên). Tang của góc giữa đường thẳng SC và mặt phẳng (SAB) bằng

Cho m là một tham số thực và hai tập hợp A=[1-2m;m+3], $\mathrm{B}=\mathrm{x}\in \mathrm{R}|\mathrm{x}\ge 8-5\mathrm{m}$. Tất cả các giá trị m để $\mathrm{A}\cap \mathrm{B}=\varnothing$ là: 

Một đội văn nghệ có 20 người, trong đó có 10 nam và 10 nữ. Hỏi có bao nhiêu cách chọn ra 5 người sao cho có ít nhất 2 nam và ít nhất 1 nữ trong 5 người đó.

Cho hàm số y = f(x) có bảng biến thiên như sau.

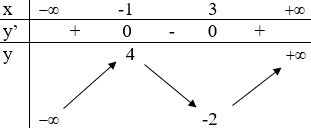
Số nghiệm của phương trình ${\mathrm{f}}^2\left(\mathrm{x}\right) -4 = 0$ là

Tổng tất cả các hệ số của khai triển ${\left(\frac{1}{\mathrm{x}}+{\mathrm{x}}^3\right)}^{\mathrm{n}}$ bằng 1024. Tìm hệ số của số hạng chứa ${\mathrm{x}}^6$ trong khai triển biểu thức trên

Phương trình (sinx - cosx)(sinx + 2cosx - 3) = 0 có tất cả bao nhiêu nghiệm thực thuộc khoảng $\left(\frac{-3\mathrm{\pi }}{4};\mathrm{\pi }\right)$ ?

Cho số phức z thỏa mãn (1+z)(1+i)-5+i=0. Số phức w=1+z bằng 

${\lim }_{\mathrm{x}\to -4}\frac{{\mathrm{x}}^2+3\mathrm{x}-4}{{\mathrm{x}}^2+4\mathrm{x}}$ bằng 

Cho hình hộp ABCD.A' B' C' D'. Mệnh đề nào sau đây sai?

Cho hai lực $\overrightarrow{{\mathrm{F}}_1}=\overrightarrow{\mathrm{MA}};\overrightarrow{{\mathrm{F}}_2}=\overrightarrow{\mathrm{MB}}$ cùng tác động vào một vật tại điểm M cường độ hai lực lần lượt là 300N và 400N, $\widehat{\mathrm{AMB}}={90}^0$. Tìm cường độ của lực tổng hợp tác động vào vật

Trong giờ Thể dục, tổ 1 của lớp 12A1 có 12 học sinh gồm 5 nam và 7 nữa tập trung ngẫu nhiên thành một hàng dọc. Tính xác suất để người đứng đầu hàng và cuối hàng đều là nữ.

Cho hàm số f(x) xác định trên R thỏa mãn f' (x)=$\sqrt{{\mathrm{e}}^{\mathrm{x}}+{\mathrm{e}}^{-\mathrm{x}}-2}$, f(0)=5 và $\text{f}\left(\ln \frac{1}{4}\right)=0$ .Giá trị của biểu thức $\mathrm{S}= \mathrm{f}\left(-\ln 6\right)+\mathrm{f}\left(\ln 4\right)$ bằng: 

Cho hàm số y=f(x) xác định và liên tục trên [1;e] thỏa mãn ${\mathrm{xf}}^{\text{'}}\left(\mathrm{x}\right)=\mathrm{x}\left[\mathrm{f}\right(\mathrm{x}){]}^2+3\mathrm{f}(\mathrm{x})+\frac{4}{\mathrm{x}}$ và f(1) = -3. Tính f(e). 

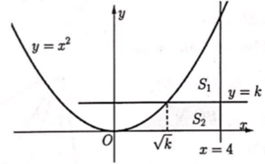
Cho hình phẳng (H) giới hạn bởi các đường y = ${\mathrm{x}}^2$, y = 0, x - 4. Đường thẳng y = k (0<k<16) chia hình (H) thành hai phần có diện tích S₁, S₂ (hình vẽ). Tìm k để S₁ = S₂.