Cho hình hộp có thể tích bằng 1. Gọi M là điểm thỏa mãn và N là trung điểm của DD’. Mặt phẳng (AMN) chia hình hộp thành hai phần, thể tích phần có chứa điểm A’ bằng
A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack
Chọn D.
Phương pháp:
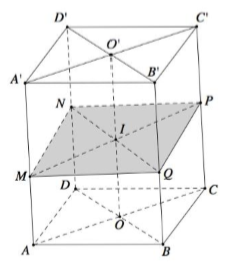

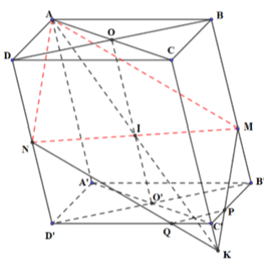
Gọi O, O’ lần lượt là tâm của các hình bình hành ABCD, A’B’C’D’.
Trong (BDD’B’), gọi I là giao điểm của OO’ và MN
Trong (ACC’A’), gọi K là giao điểm của AI và CC’
Trong (CDD’C’), gọi Q là giao điểm của NK và C’D’
Trong (CBB’C’), gọi P là giao điểm của MK và C’B’
=> Thiết diện của hình hộp cắt bởi mặt phẳng (AMN) là ngũ giác AMPQN.



Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho hàm số với m là tham số thực. Có bao nhiêu giá trị nguyên của tham số để hàm số có 5 điểm cực trị
Thể tích của một khối lăng trụ có đường cao bằng 3a diện tích mặt đáy bằng là:
Cho hàm số Tập hợp các giá trị của tham số m để hàm số nghịch biến trên là [a;b]. Khi đó a - 3b bằng
Trong không gian Oxyz, phương trình tham số của đường thẳng đi qua điểm M(2;0;-1) và có vecto chỉ phương là
Cho hàm số f(x) liên tục trên R có đạo hàm thỏa mãn và Tích phân bằng
Cho số phức . Điểm biểu diễn số phức z trong mặt phẳng Oxy có tọa độ là:
Gọi M và N là giao điểm của đồ thị hai hàm số . Tọa độ trung điểm I của đoạn thẳng MN là
Một bạn học sinh có 3 cái quần khác nhau và 2 cái áo khác nhau. Hỏi bạn học sinh đó có bao nhiêu cách lựa chọn 1 bộ quần áo.
Ba người A, B, C đi săn độc lập với nhau, cùng nổ súng bắn vào mục tiêu. Biết rằng xác suất bắn trúng mục tiêu của A, B, C tương ứng là 0,7; 0,6; 0,5. Xác suất để có ít nhất một người bắn trúng là: