Có tất cả bao nhiêu giá trị thực của tham số m để đường thẳng cắt đồ thị tại ba điểm phân biệt sao cho tam giác AOC vuông tại ?
A. 0
B. 1
C. 3
D. 2
 Giải bởi Vietjack
Giải bởi Vietjack
Phương pháp:
+ Xét phương trình hoành độ giao điểm của d và đồ thị (C)
+ Lập luận để phương trình này có ba nghiệm phân biệt.

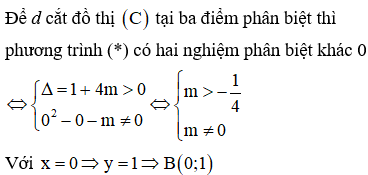

Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho hai hàm số và (với m là tham số). Hỏi phương trình có bao nhiêu nghiệm?
Đường thẳng y = m tiếp xúc với đồ thị tại hai điểm phân biệt . Giá trị của biểu thức .
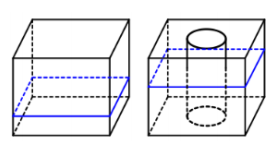
Một hình hộp chữ nhật có chiều cao là 90cm, đáy hình hộp là hình chữ nhật có chiều rộng là 50cm và chiều dài là 80cm. Trong khối hộp có chứa nước, mực nước so với đáy hộp có chiều cao là 40cm. Hỏi khi đặt vào khối hộp một khối trụ có chiều cao bằng chiều cao khối hộp và bán kính đáy là 20cm theo phương thẳng đứng thì chiều cao của mực nước so với đáy là bao nhiêu?
Có bao nhiêu cách phân tích số thành tích của ba số nguyên dương, biết rằng các cách phân tích mà các nhân tử chỉ khác nhau về thứ tự thì chỉ được tính một lần?
Cho một hộp có chứa 5 bóng xanh, 6 bóng đỏ và 7 bóng vàng. Lấy ngẫu nhiên 4 bóng từ hộp, tính xác suất để có đủ 3 màu.
Cho dãy số là một cấp số cộng, biết . Tính tổng của 22 số hạng đầu tiên của dãy.
Cho lăng trụ tứ giác đều có đáy là hình vuông cạnh a, chiều cao 2a. Tính thể tích khối lăng trụ.
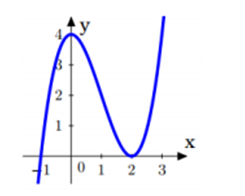
Cho hàm số có đồ thị (C) như hình vẽ bên và đường thẳng (với m là tham số). Hỏi có bao nhiêu giá trị nguyên của tham số m để đường thẳng d cắt đồ thị (C) tại ba điểm phân biệt
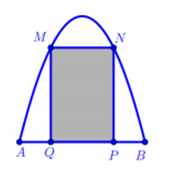
Một chiếc cổng có hình dạng là một Parabol có khoảng cách giữa hai chân cổng là AB = 8m. Người ta treo một tấm phông hình chữ nhật có hai đỉnh M, N nằm trên Parabol và hai đỉnh P, Q nằm trên mặt đất (như hình vẽ). Ở phần phía ngoài phông (phần không tô đen) người ta mua hoa để trang trí với chi phí cho 1m2 cần số tiền mua hoa là 200.000 đồng cho Biết MN = 4m; MQ = 6m. Hỏi số tiền dùng để mua hoa trang trí chiếc cổng gần với số tiền nào sau đây?
Cho hàm số y = f(x) xác định, liên tục trên R và có bảng biến thiên như sau:
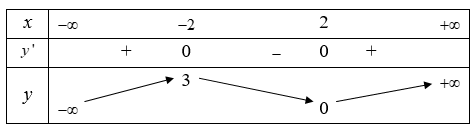
Tìm giá trị cực đại và giá trị cực tiểu của hàm số đã cho.
Tìm hệ số của số hạng chứa trong khai triển nhị thức Newton của biểu thức