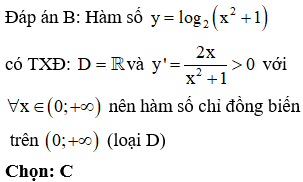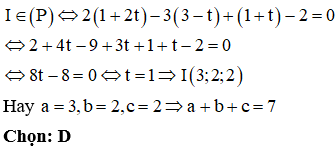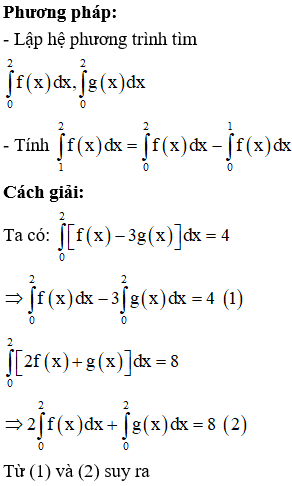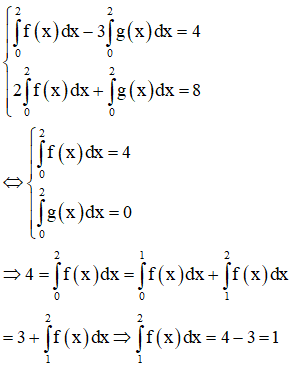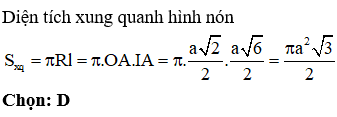50 câu hỏi trắc nghiệm thuộc Tổng hợp 20 đề thi thử thpt quốc gia môn Toán cực hay có lời giải chi tiết abc - đề 12

Câu 1:

Cho số phức $\bar{z} = 3 + 2 i$ . Tìm phần thực và phần ảo của số phức z.

A. Phần thực bằng -3, phần ảo bằng 2.

B. Phần thực bằng 3, phần ảo bằng 2.

C. Phần thực bằng 3, phần ảo bằng -2 .

D. Phần thực bằng -3, phần ảo bằng -2.

Xem đáp án

Câu 2:

Trong hệ tọa độ Oxyz, cho đường thẳng $Δ = \frac{x - x_{0}}{a} = \frac{y - y_{0}}{b} = \frac{z - z_{0}}{c}$ . Điểm M nằm trên $Δ$ thì điểm M có dạng nào sau đây?

A. $M (a t; b t; c t)$

B. $M (x_{0} t; y_{0} t; z_{0} t)$

C. $M (a + x_{0} t; b + y_{0} t; c + z_{0} t)$

D. $M (x_{0} + a t; y_{0} + b t; z_{0} + c t)$

Xem đáp án

Phương pháp:

Biến đổi phương trình chính tắc của $Δ$ về dạng tham số từ đó suy ra tọa độ điểm M .

Cách giải:

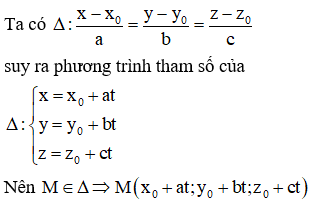
Chọn: D

Câu 3:

Cho hàm số y = f(x) xác định, liên tục trên R và có bảng biến thiên như sau:

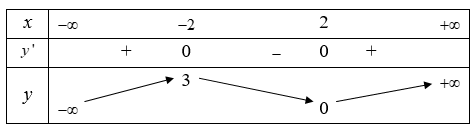
Tìm giá trị cực đại $y_{C Đ}$ và giá trị cực tiểu $y_{C T}$ của hàm số đã cho.

A. $y_{C Đ} = - 2 v à y_{C T} = 2$

B. $y_{C Đ} = 3 v à y_{C T} = 0$

C. $y_{C Đ} = 2 v à y_{C T} = 0$

D. $y_{C Đ} = 3 v à y_{C T} = - 2$

Xem đáp án

Phương pháp:

Quan sát bảng biến thiên và tìm điểm cực đại, cực tiểu và các giá trị cực đại, cực tiểu tương ứng.

Cách giải:

Số cách chọn là: 6.4 = 24 (cách). Quan sát bảng biến thiên ta thấy:

Hàm số đạt cực đại tại x = 2 và y_CD = 3 .

Hàm số đạt cực tiểu tại x = 2 và y_CT = 0 .

Vậy y_CD = 3 và y_CT = 0 .

Chọn: B

Câu 4:

Trong hệ tọa độ Oxyz, cho ba điểm $A (1; 0; 0); B (0; - 1; 0); C (0; 0; 2)$ . Phương trình mặt phẳng (ABC) là

A. $x - 2 y + z = 0$

B. $x - y + \frac{z}{2} = 1$

C. $x + \frac{y}{2} - z = 1$

D. $2 x - y + z = 0$

Xem đáp án

Phương pháp:

Cách 1 : Sử dụng phương trình mặt phẳng theo đoạn chắn :

Mặt phẳng (P) cắt ba trục Ox; Oy; Oz lần lượt tại ba điểm

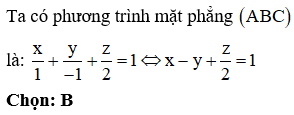
Câu 5:

Đường thẳng y = m tiếp xúc với đồ thị $(C) : y = - 2 x^{4} + 4 x^{2} - 1$ tại hai điểm phân biệt $A (x_{A}; y_{A}) v à B (x_{B}; y_{B})$ . Giá trị của biểu thức $y_{A} + y_{B}$ .

A. 2

B. -1

C. 1

D. 0

Xem đáp án

Phương pháp:

Nhận xét tính chất của đường thẳng y = m dựa vào điều kiện tiếp xúc với đồ thị hàm số tại hai điểm phân biệt.

Cách giải:

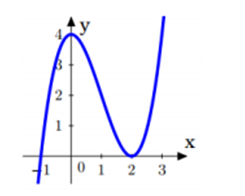
Đồ thị hàm số (C) có dạng:

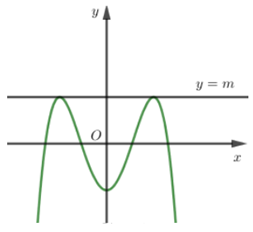
Quan sát dáng đồ thị ta thấy, nếu đường thẳng y = m tiếp xúc với đồ thị hàm số (C) tại hai điểm phân biệt thì chúng phải là hai điểm cực đại của đồ thị hàm số.

Câu 6:

Trong các hàm số dưới đây, hàm số nào đồng biến trên tập R?

A. $y = 2^{1 - 3 x}$

B. $y = \log_{2} (x - 1)$

C. $y = \log_{2} (2^{x} + 1)$

D. $y = \log_{2} (x^{2} + 1)$

Xem đáp án

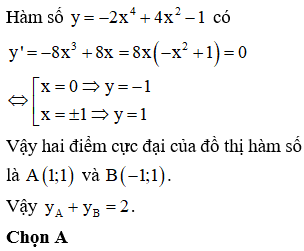
Câu 7:

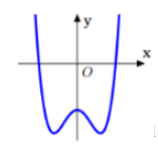
Đường cong như hình bên là đồ thị của hàm số nào sau đây?

A. $y = - x^{3} + 3 x^{2} - 2$

B. $y = x^{3} - 3 x^{2} - 2$

C. $y = x^{4} - 2 x^{2} - 2$

D. $y = - x^{4} + 2 x^{2} - 2$

Xem đáp án

Phương pháp:

Sử dụng khai triển nhị thức Newton: Quan sát đồ thị hàm số, nhận xét dáng điệu và đối chiếu với các dáng đồ thị hàm số ở mỗi đáp án.

Cách giải:

Quan sát đồ thị hàm số ta thấy đây là đồ thị hàm bậc bốn trùng phương, loại A và B.

Câu 8:

Tìm tập xác định của hàm số $y = {(x^{2} + 2 x - 3)}^{e}$

A. $(- \infty; - 3) \cup (1; + \infty)$

B. $(- \infty; - 3] \cup [3; + \infty)$

C. $(- 3; - 1)$

D. [-3;-1]

Xem đáp án

Câu 9:

Cho hàm số $y = \frac{2 x + 1}{x + 1}$ . Mệnh đề đúng là

A. Hàm số nghịch biến trên $(- \infty; - 1) v à (1; + \infty)$

B. Hàm số đồng biến trên $(- \infty; - 1) v à (1; + \infty)$ , nghịch biến trên $(- 1; 1)$

C. Hàm số đồng biến trên R.

D. Hàm số đồng biến trên $(- \infty; - 1) v à (- 1; + \infty)$

Xem đáp án

Câu 10:

Thể tích khối cầu bán kính R là

A. $π R^{3}$

B. $\frac{4 π R^{3}}{3}$

C. $2 π R^{3}$

D. $\frac{π R^{3}}{3}$

Xem đáp án

Câu 11:

Cho $f (x), g (x)$ là các hàm số có đạo hàm liên tục trên $ℝ, k \in ℝ$ . Trong các khẳng định dưới đây, khẳng định nào sai?

A. $\int [f (x) - g (x)] d x = \int f (x) d x - \int g (x) d x$

B. $\int f' (x) d x = f (x) + C$

C. $\int k f (x) d x = k \int f (x) d x$

D. $\int [f (x) + g (x)] d x = \int f (x) d x + \int g (x) d x$

Xem đáp án

Phương pháp:

Sử dụng định lí Vi-ét. Sử dụng công thức tính thể tích khối cầu

Cách giải:

Đáp án A, D đúng theo tính chất tổng, hiệu các nguyên hàm.

Đáp án B đúng theo nhận xét về định nghĩa nguyên hàm.

Đáp án C sai, tính chất này chỉ đúng với k > 0 .

Chọn: C

Câu 12:

Cho lăng trụ tứ giác đều có đáy là hình vuông cạnh a, chiều cao 2a. Tính thể tích khối lăng trụ.

A. $\frac{2 a^{3}}{3}$

B. $\frac{4 a^{3}}{3}$

C. $a^{3}$

D. $2 a^{3}$

Xem đáp án

Phương pháp:

Thể tích khối lăng trụ có diện tích đáy S và chiều cao h là V = h.S

Cách giải:

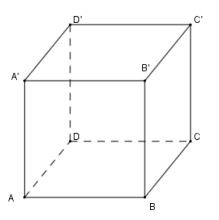
Diện tích đáy lăng trụ là S = a²

Thể tích lăng trụ là V = h.S = 2a.a² = 2a³

Chọn: D

Câu 13:

Tích của giá trị lớn nhất và giá trị nhỏ nhất của hàm số $f (x) = x + \frac{4}{x}$ trên đoạn [1;3] bằng

A. $\frac{65}{3}$

B. 20

C. 6

D. $\frac{52}{3}$

Xem đáp án

Câu 14:

Trong hệ tọa độ Oxyz, cho hai đường thẳng chéo nhau $d_{1} : \frac{x - 2}{2} = \frac{y + 2}{1} = \frac{z - 6}{- 2} v à d_{2} : \frac{x - 4}{1} = \frac{y + 2}{- 2} = \frac{z + 1}{3}$ . Phương trình mặt phẳng (P) chứa $d_{1}$ và song song với $d_{2}$ là:

A. $(P) : x + 8 y + 5 z + 16 = 0$

B. $(P) : x + 8 y + 5 z - 16 = 0$

C. $(P) : 2 x + y - 6 = 0$

D. $(P) : x + 4 y + 3 z - 12 = 0$

Xem đáp án

+ Lấy điểm M $\in$ d₁ => M $\in$ (P)

Câu 15:

Trong hệ tọa độ Oxyz, cho đường thẳng $d : \frac{x - 1}{2} = \frac{y - 3}{- 1} = \frac{z - 1}{1}$ cắt mặt phẳng $(P) : 2 x - 3 y + z - 2 = 0$ tại điểm I(a;b;c). Khi đó a+b+c bằng

A. 9

B. 5

C. 3

D. 7

Xem đáp án

Câu 16:

Cho dãy số $(u_{n})$ là một cấp số cộng, biết $u_{2} + u_{21} = 50$ . Tính tổng của 22 số hạng đầu tiên của dãy.

A. 2018

B. 550

C. 1100

D. 50

Xem đáp án

Câu 17:

Số đường tiệm cận của đồ thị hàm số $y = \frac{x + 1}{|x| - 2 x + 1}$ là

A. 4

B. 3

C. 2

D. 1

Xem đáp án

Phương pháp:

- Xét điều kiện của x phá dấu giá trị tuyệt đối đưa hàm số về dạng khoảng.

- Tìm các đường tiệm cận của mỗi hàm số có được và kết luận.

Cách giải:

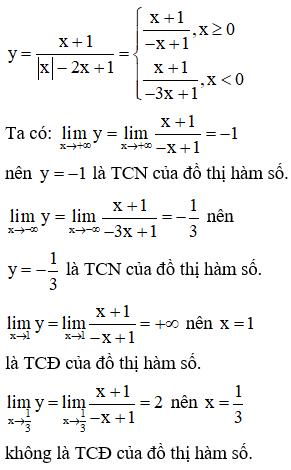
Vậy đồ thị hàm số chỉ có 3 đường tiệm cận.

Chọn: B

Câu 18:

Cho khối chóp S.ABC có đáy ABC là tam giác đều cạnh a, tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy. Tính theo a thể tích khối chóp S.ABC

A. $V = \frac{a^{3}}{8}$

B. $V = \frac{a^{3} \sqrt{3}}{3}$

C. $V = \frac{a^{3} \sqrt{3}}{4}$

D. $V = \frac{a^{3}}{4}$

Xem đáp án

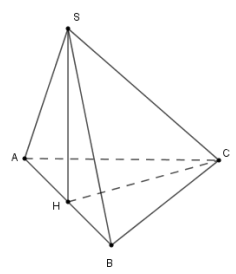
Vì SHlà đường trung tuyến trong tam giác SAB đều cạnh a nên

Câu 19:

Họ nguyên hàm của hàm số $f (x) = 2 x (1 + 3 x^{3})$ là

A. $x^{2} (1 + \frac{3}{2} x^{2}) + C$

B. $x^{2} (1 + \frac{6 x^{3}}{5}) + C$

C. $2 x (x + \frac{3}{4} x^{4}) + C$

D. $x^{2} (x + \frac{3}{4} x^{3}) + C$

Xem đáp án

Câu 20:

Tìm tập nghiệm S của bất phương trình ${(\frac{2}{5})}^{1 - 3 x} \geq \frac{25}{4}$ .

A. $S = [1; + \infty)$

B. $[\frac{1}{3}; + \infty)$

C. $(- \infty; \frac{1}{3})$

D. $(- \infty; 1]$

Xem đáp án

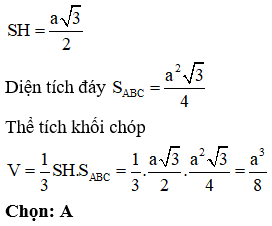
Câu 21:

Trong hệ tọa độ Oxyz, cho điểm $A (3; 5; 3)$ và hai mặt phẳng $(P) : 2 x + y + 2 z - 8 = 0, (Q) : x - 4 y + z - 4 = 0$ . Viết phương trình đường thẳng d đi qua A và song song với cả hai mặt phẳng (P), (Q).

A. $d : \{\begin{cases} x = 3 + t \\ y = 5 - t \\ z = 3 \end{cases}$

B. $d : \{\begin{cases} x = 3 \\ y = 5 + t \\ z = 3 - t \end{cases}$

C. $d : \{\begin{cases} x = 3 + t \\ y = 5 \\ z = 3 - t \end{cases}$

D. $d : \{\begin{cases} x = 3 + t \\ y = 5 \\ z = 3 + t \end{cases}$

Xem đáp án

Phương pháp:

Đường thẳng d song song với cả hai mặt phẳng (P), (Q)

Câu 22:

Trong hệ tọa độ Oxyz, cho điểm $A (- 1; 1; 6)$ và đường thẳng $Δ : \{\begin{cases} x = 2 + t \\ y = 1 - 2 t \\ z = 2 t \end{cases}$ . Hình chiếu vuông góc của A trên $Δ$ là

A. $M (3; - 1; 2)$

B. $H (11; - 17; 18)$

C. $N (1; 3; - 2)$

D. $K (2; 1; 0)$

Xem đáp án

Chọn: A

Câu 23:

Cho f(x), g(x) là các hàm số liên tục trên R thỏa mãn $\int_{0}^{1} f (x) d x = 3, \int_{0}^{2} [f (x) - 3 g (x)] d x = 4 v à \int_{0}^{2} [2 f (x) + g (x)] d x = 8$ . Tính $\int_{1}^{2} f (x) d x$

A. I = 1

B. I = 2

C. I = 3

D. I = 0

Xem đáp án

Câu 24:

Đồ thị hàm số $y = - \frac{x^{4}}{2} + x^{2} + \frac{3}{2}$ cắt trục hoành tại mấy điểm?

A. 0

B. 2

C. 4

D. 3

Xem đáp án

Câu 25:

Trong hệ tọa độ Oxyz, cho điểm $I (2; - 1; - 1)$ và mặt phẳng $(P) : x - 2 y - 2 z + 3 = 0$ . Viết phương rình mặt cầu (S) có tâm I và tiếp xúc với mặt phẳng (P)

A. $(S) = x^{2} + y^{2} + z^{2} - 4 x + 2 y + 2 z - 3 = 0$

B. $(S) = x^{2} + y^{2} + z^{2} - 2 x + y + z - 3 = 0$

C. $(S) = x^{2} + y^{2} + z^{2} - 4 x + 2 y + 2 z + 1 = 0$

D. $(S) = x^{2} + y^{2} + z^{2} - 2 x + y + z + 1 = 0$

Xem đáp án

Câu 26:

Cho hình lập phương $A B C D . A' B' C' D'$ có cạnh bằng a. Một hình nón có đỉnh là tâm của hình vuông $A' B' C' D'$ và có đường tròn đáy ngoại tiếp hình vuông ABCD. Tính diện tích xung quanh của hình nón đó.

A. $\frac{π a^{2} \sqrt{2}}{2}$

B. $π a^{2} \sqrt{3}$

C. $\frac{π a^{2} \sqrt{2}}{4}$

D. $\frac{π a^{2} \sqrt{3}}{2}$

Xem đáp án

Câu 27:

Tìm hệ số của số hạng chứa $x^{9}$ trong khai triển nhị thức Newton của biểu thức ${(3 + x)}^{11}$

A. 9

B. 110

C. 495

D. 55

Xem đáp án

Câu 28:

Cho số thực $a > 0; a \neq 1$ . Giá trị của $\log_{a^{2}} (\sqrt[7]{a^{3}})$ bằng

A. $\frac{3}{14}$

B. $\frac{6}{7}$

C. $\frac{3}{8}$

D. $\frac{7}{6}$

Xem đáp án

Câu 29:

Đạo hàm của hàm số $y = \log_{8} (x^{3} - 3 x - 4)$ là

A. $\frac{3 x^{3} - 3}{(x^{3} - 3 x - 4) \ln 2}$

B. $\frac{x^{2} - 1}{(x^{3} - 3 x - 4) \ln 2}$

C. $\frac{3 x^{3} - 3}{x^{3} - 3 x - 4}$

D. $\frac{1}{(x^{3} - 3 x - 4) \ln 8}$

Xem đáp án

Câu 30:

Cho cấp số nhân $(u_{n})$ thỏa mãn $\{\begin{cases} u_{1} + u_{3} = 10 \\ u_{4} + u_{6} = 80 \end{cases}$ . Tìm $u_{3}$

A. $u_{3} = 8$

B. $u_{3} = 2$

C. $u_{3} = 6$

D. $u_{3} = 4$

Xem đáp án

Câu 31:

Cho khối nón (N) đỉnh S, chiều cao là $a \sqrt{3}$ và độ dài đường sinh là 3a. Mặt phẳng (P) đi qua đỉnh S, cắt và tạo với mặt đáy của khối nón một góc $60^{0}$ . Tính diện tích thiết diện tạo bởi mặt phẳng (P) và khối nón (N)

A. $2 a^{2} \sqrt{5}$

B. $a^{2} \sqrt{3}$

C. 2 $a^{2} \sqrt{3}$

D. $a^{2} \sqrt{5}$

Xem đáp án

Phương pháp:

Xác định góc giữa hai mặt phẳng và tính toán dựa vào các kiến thức hình học đã biết.

Cách giải:

Câu 32:

Cho hàm số $y = x^{3} - 3 x^{2} + 4$ có đồ thị (C) như hình vẽ bên và đường thẳng $d : y = m^{3} - 3 m^{2} + 4$ (với m là tham số). Hỏi có bao nhiêu giá trị nguyên của tham số m để đường thẳng d cắt đồ thị (C) tại ba điểm phân biệt

A. 3

B. 1

C. 2

D. Vô số

Xem đáp án

Câu 33:

Cho các số phức z thỏa mãn $|z| = 2$ . Biết rằng tập hợp các điểm biểu diễn số phức $w = 3 - 2 i + (4 - 3 i) z$ là một đường tròn. Tính bán kính r của đường tròn đó

A. $r = 5$

B. $r = 2 \sqrt{5}$

C. r = 10

D. r = 20

Xem đáp án

Câu 34:

Cho $9^{x} + 9^{- x} = 14$ , khi đó biểu thức $M = \frac{2 + 81^{x} + 81^{- x}}{11 - 3^{x} - 3^{- x}}$ có giá trị bằng:

A. 14

B. 49

C. 42

D. 28

Xem đáp án

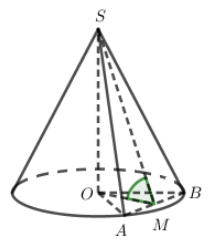
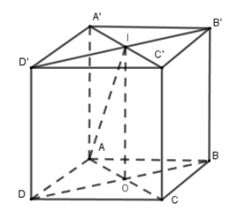
Câu 35:

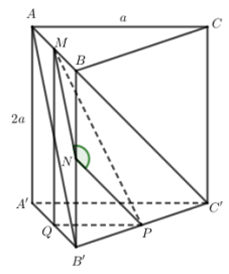
Cho lăng trụ tam giác đều $A B C . A' B' C'$ có đáy là tam giác đều cạnh $a, A A' = 2 a$ . Gọi $α$ là góc giữa AB' và BC'. Tính $\cos α$

A. $\cos α = \frac{5}{8}$

B. $\cos α = \frac{\sqrt{51}}{10}$

C. $\cos α = \frac{\sqrt{39}}{8}$

D. $\cos α = \frac{7}{10}$

Xem đáp án

Phương pháp:

- Gọi M, N, P lần lượt là trung điểm của $A B', B B', B' C'$

- Sử dụng tính chất góc giữa hai đường chéo nhau bằng góc giữa hai đường thẳng cùng thuộc 1 mặt phẳng mà lần lượt song song với hai đường thẳng đã cho.

Cách giải:

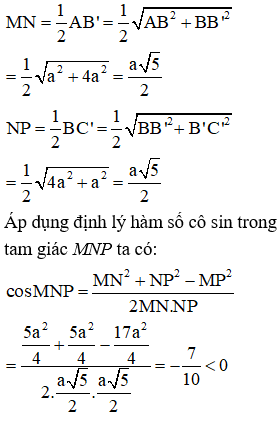
Câu 36:

Cho hai đường thẳng $d_{1} : \{\begin{cases} x = 1 + t \\ y = 2 - t \\ z = 3 + 2 t \end{cases} v à d_{2} : \frac{x - 1}{2} = \frac{y - m}{1} = \frac{z + 2}{- 1}$ (với m là tham số). Tìm m để hai đưởng thẳng $d_{1}; d_{2}$ cắt nhau.

A. m = 4

B. m = 9

C. m = 7

D. m = 5

Xem đáp án

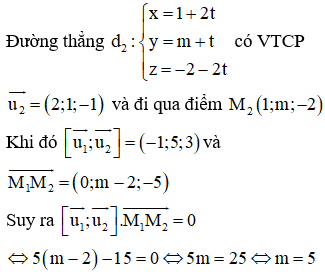
Chọn: D

Câu 37:

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy. Tính khoảng cách từ điểm C đến mặt phẳng (SAD).

A. $\frac{a \sqrt{3}}{6}$

B. $\frac{a \sqrt{3}}{2}$

C. $\frac{a \sqrt{3}}{3}$

D. $\frac{a \sqrt{3}}{4}$

Xem đáp án

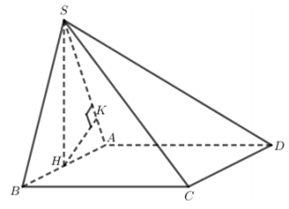
Chọn: B

Câu 38:

Cho một hộp có chứa 5 bóng xanh, 6 bóng đỏ và 7 bóng vàng. Lấy ngẫu nhiên 4 bóng từ hộp, tính xác suất để có đủ 3 màu.

A. $\frac{35}{816}$

B. $\frac{35}{68}$

C. $\frac{175}{5832}$

D. $\frac{35}{1632}$

Xem đáp án

Phương pháp:

Chia các trường hợp để tính số phần tử của biến cố: “4 quả bóng có đủ 3 màu”

Câu 39:

Cho phương trình $\log_{3}^{2} x - 4 \log_{3} x + m - 3 = 0$ . Tìm tất cả các giá trị nguyên của tham số m để phương trình đã cho có hai nghiệm phân biệt thỏa mãn $x_{1} > x_{2} > 1$

A. 6

B. 4

C. 3

D. 5

Xem đáp án

Chọn: C

Câu 40:

Có tất cả bao nhiêu giá trị thực của tham số m để đường thẳng $d : y = m x + 1$ cắt đồ thị $(C) : x^{3} - x^{2} + 1$ tại ba điểm $A; B (0; 1); C$ phân biệt sao cho tam giác AOC vuông tại $O (0; 0)$ ?

A. 0

B. 1

C. 3

D. 2

Xem đáp án

Phương pháp:

+ Xét phương trình hoành độ giao điểm của d và đồ thị (C)

+ Lập luận để phương trình này có ba nghiệm phân biệt.

Câu 41:

Trong hệ tọa độ Oxyz, cho điểm $M (1; - 1; 2)$ và hai đường thẳng $d_{1} : \{\begin{cases} x = t \\ y = 1 - t \\ z = - 1 \end{cases}, d_{2} : \frac{x + 1}{2} = \frac{y - 1}{1} = \frac{z + 2}{1}$ . Đường thẳng $∆$ đi qua M và cắt cả hai đường thẳng $d_{1}, d_{2}$ có véc tơ chỉ phương là $\vec{u_{Δ}} (1; a; b)$ , tính a + b

A. $a + b = - 1$

B. $a + b = - 2$

C. $a + b = 2$

D. $a + b = 1$

Xem đáp án

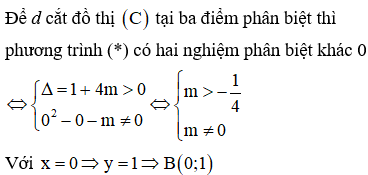
Câu 42:

Hai người A và B ở cách nhau 180m trên một đoạn đường thẳng và cùng chuyển động thẳng theo một hướng với vận tốc biến thiên theo thời gian, A chuyện động với vận tốc $v_{1} (t) = 6 t + 5 (m / s)$ , B chuyển động với vận tốc $v_{2} (t) = 2 a t - 3 (m / s)$ (a là hằng số), trong đó t (giây) là khoảng thời gian từ lúc A, B bắt đầu chuyển động. Biết rằng lúc đầu A đuổi theo B và sau 10 (giây) thì đuổi kịp. Hỏi sau 20 giây, A cách B bao nhiêu mét?

A. 320 (m)

B. 720 (m)

C. 360 (m)

D. 380 (m)

Xem đáp án

Vì sau 10 giây người A đuổi kịp người B và người A lúc ban đầu cách người B là 180m nên ta có phương trình

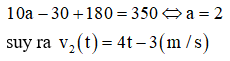
Quãng đường người A đi được trong 20 giây kể từ khi bắt đầu chuyển động là

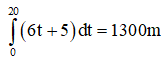
Quãng đường người B đi được trong 20 giây kể từ khi bắt đầu chuyển động là

Câu 43:

Một hình hộp chữ nhật có chiều cao là 90cm, đáy hình hộp là hình chữ nhật có chiều rộng là 50cm và chiều dài là 80cm. Trong khối hộp có chứa nước, mực nước so với đáy hộp có chiều cao là 40cm. Hỏi khi đặt vào khối hộp một khối trụ có chiều cao bằng chiều cao khối hộp và bán kính đáy là 20cm theo phương thẳng đứng thì chiều cao của mực nước so với đáy là bao nhiêu?

A. 68,32cm

B. 78,32cm

C. 58,32cm

D. 48,32cm

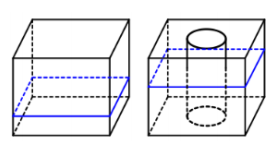
Xem đáp án

Phương pháp:

- Tính thể tích lượng nước trong khối hộp chữ nhật.

- Gọi h là chiều cao mới, lập phương trình ẩn h với chú ý lượng nước trong hộp là không đổi.

Cách giải:

Thể tích nước trước khi đưa khối trụ vào là: $V_{n} = 40.50.80 = 160000 c m^{3}$

Gọi h là chiều cao của mực nước sau khi đặt khối trụ vào.

Khi đó thể tích khối hộp chữ nhật chiều cao h là $V_{1} = 50.80. h = 4000 h$

Thể tích khối trụ có chiều cao h là

Câu 44:

Một chiếc cổng có hình dạng là một Parabol có khoảng cách giữa hai chân cổng là AB = 8m. Người ta treo một tấm phông hình chữ nhật có hai đỉnh M, N nằm trên Parabol và hai đỉnh P, Q nằm trên mặt đất (như hình vẽ). Ở phần phía ngoài phông (phần không tô đen) người ta mua hoa để trang trí với chi phí cho 1m² cần số tiền mua hoa là 200.000 đồng cho $1 m^{2}$ Biết MN = 4m; MQ = 6m. Hỏi số tiền dùng để mua hoa trang trí chiếc cổng gần với số tiền nào sau đây?

A. 3.735.300 đồng

B. 3.347.300 đồng

C. 3.734.300 đồng

D. 3.733.300 đồng

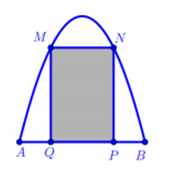
Xem đáp án

Phương pháp:

+ Tìm phương trình Parabol

+ Diện tích hình phẳng giới hạn bởi

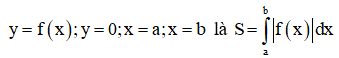
+ Tính diện tích hình chữ nhật từ đó tính diện tích phần trồng hoa và tính số tiền cần dùng để mua hoa trang trí.

Cách giải:

Gắn hệ trục tọa độ Oxy như hình vẽ, ta có Parabol đi qua các điểm $A (4; 0); N (2; 6)$

Hoành độ giao điểm của Parabol và trục hoành là

Câu 45:

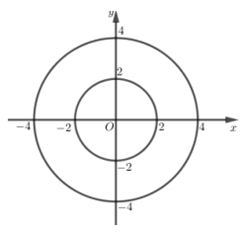
Cho hai số phức z, w thay đổi thỏa mãn $|z| = 3, |z - w| = 1$ . Biết tập hợp điểm của số phức w là hình phẳng H. Tính diện tích S của hình H.

A. $S = 20 π$

B. $S = 12 π$

C. $S = 4 π$

D. $S = 16 π$

Xem đáp án

Phương pháp:

Sử dụng phương pháp hình học: Tìm tập hợp các điểm biểu diễn số phức z, w và tính toán.

Cách giải:

Câu 46:

Cho $\int_{0}^{1} \frac{9^{x} + 3 m}{9^{x} + 3} d x = m^{2} - 1$ . Tính tổng tất cả các giá trị của tham số m.

A. $P = 12$

B. $P = \frac{1}{2}$

C. P = 16

D. P = 24

Xem đáp án

Từ đó giải phương trình ẩn m thu được để tìm m.

Cách giải:

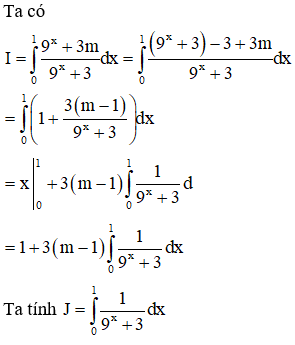
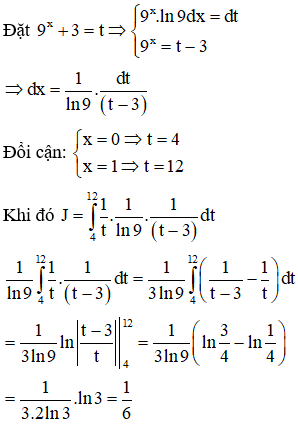
Câu 47:

Có bao nhiêu cách phân tích số $15^{9}$ thành tích của ba số nguyên dương, biết rằng các cách phân tích mà các nhân tử chỉ khác nhau về thứ tự thì chỉ được tính một lần?

A. 517

B. 516

C. 493

D. 492

Xem đáp án

Phương pháp:

Chia làm ba trường hợp:

+) 3 số giống nhau.

+) 2 trong ba số giống nhau.

+) 3 số đôi một khác nhau.

Cách giải:

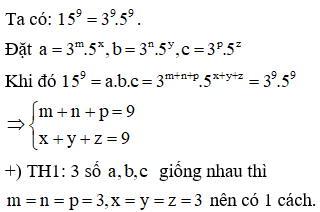
+) TH2: 2 trong ba số giống nhu và khác số còn lại, giả sử

Câu 48:

Cho các số thực a, b > 1 thỏa mãn $a^{\log_{b} a} + 16 b^{\log_{a} (\frac{b^{8}}{a^{3}})} = 12 b^{2}$ giá trị của biểu thức $P = a^{3} + b^{3}$ là

A. P = 20

B. P = 39

C. P = 125

D. P = 72

Xem đáp án

Chọn: D

Câu 49:

Cho hình chóp S.ABCD có đáy ABCD là hình vuông, hình chiếu vuông góc của đỉnh S xuống mặt đáy nằm trong hình vuông ABCD. Hai mặt phẳng (SAD), (SBC) vuông góc với nhau; góc giữa hai mặt phẳng $(S A B) v à (S A C)$ là $60 °;$ góc giữa hai mặt phẳng $(S A B) v à (S A D)$ là $45 °$ Gọi $α$ là góc giữa hai mặt phẳng $(S A B) v à (A B C D)$ , tính cos $α$

A. $\cos α = \frac{1}{2}$

B. $\cos α = \frac{\sqrt{2}}{2}$

C. $\cos α = \frac{\sqrt{3}}{2}$

D. $\cos α = \frac{\sqrt{2}}{3}$

Xem đáp án

Phương pháp:

- Sử dụng phương pháp tọa độ trong không gian, gắn hệ trục tọa độ gốc A và các trục tọa độ sao cho

- Sử dụng các công thức điểm, véc tơ, mặt phẳng, góc giữa hai mặt phẳng để tính toán.

Cách giải:

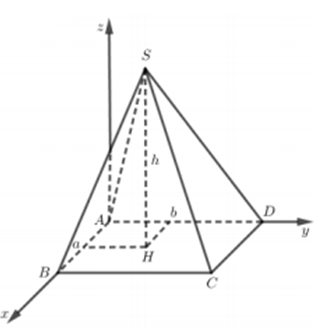
Gắn hệ trục tọa độ như hình vẽ, giả sử ABCD là hình vuông cạnh l,

chiều cao hình chóp SH = h.

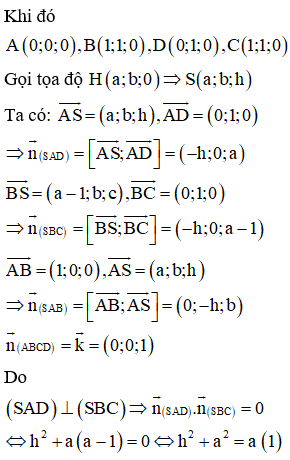
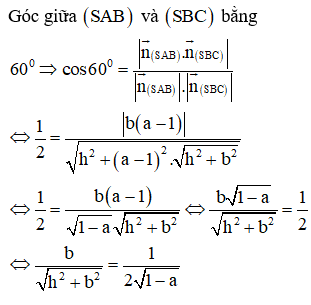
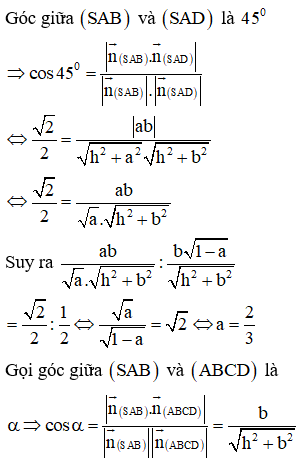
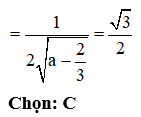
Câu 50:

Cho hai hàm số $f (x) = \frac{1}{3} x^{3} - (m + 1) x^{2} + (3 m^{2} + 4 m + 5) x + 2019$ và $g (x) = (m^{2} + 2 m + 5) x^{3} - (2 m^{2} + 4 m + 9) x^{2} - 3 x + 2$ (với m là tham số). Hỏi phương trình $g (f (x)) = 0$ có bao nhiêu nghiệm?

A. 9

B. 0

C. 3

D. 1

Xem đáp án

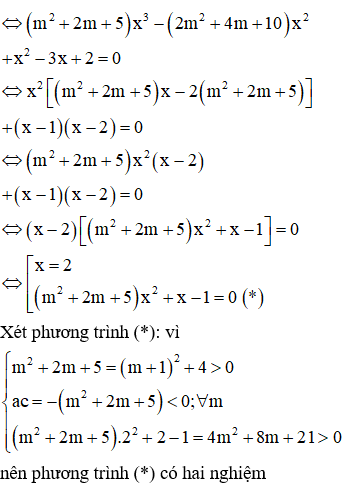
Vì f(x) là hàm đồng biến nên mỗi phương trình (1);(2);(3) đều chỉ có 1 nghiệm duy nhất và ba nghiệm của phương trình này khác nhau.

Từ đó phương trình $g (f (x)) = 0$ có ba nghiệm phân biệt.

Chọn: C

CHỌN BỘ SÁCH BẠN MUỐN XEM

Tổng hợp 20 đề thi thử thpt quốc gia môn Toán cực hay có lời giải chi tiết abc

Tổng hợp 20 đề thi thử thpt quốc gia môn Toán cực hay có lời giải chi tiết abc - đề 12

Danh sách câu hỏi

Bài thi liên quan