Phương trình nào dưới đây tương đương với phương trình $\cos 2x+\sin 3x=1+2\sin x.\cos 2x$?

Cho hình chóp S.ABC có tam giác ABC vuông cân tại B, AC = $a\sqrt{2}$, mặt phẳng (SAC) vuông góc với mặt đáy (ABC). Các mặt bên (SAB), (SBC) tạo với mặt đáy các góc bằng nhau và bằng 60$°$.Tính theo a thể tích V của khối chóp S. ABC.

Cho tứ diện ABCD có cạnh AD vuông góc với mặt phẳng (ABC),AC =AD = 4, AB =3, BC = 5. Tính khoảng cách d từ điểm A đến mặt phẳng (BCD).

Cho hình phẳng (H) giới hạn bởi các đường y = lnx, y = 0, x = k (k > 1). Tìm k để diện tích hình phẳng (H) bằng 1

Tìm nghiệm của phương trình $\frac{3^{2x-6}}{27}={\left(\frac{1}{3}\right)}^x$.

Cho tứ diện đều ABCD. Biết khoảng cách từ A đến mặt phẳng (BCD) bằng 6. Tính thể tích V tứ diện đều ABCD.

Cho hàm số $f\left(x\right)=\left\{\begin{array}{l}\frac{\sqrt{x^2+1}-1}{x} khi x\ne 0\\ 0 khi x=0\end{array}\right.$. Tính $f\text{'}\left(0\right)$?

Cho a là số thực dương. Biết rằng F(x) là một nguyên hàm của hàm số $f\left(x\right)=e^x\left(\ln \left(ax\right)+\frac{1}{x}\right)$ thỏa mãn $F\left(\frac{1}{a}\right)=0$ và $F\left(2018\right)=e^{2018}$. Mệnh đề nào sau đây đúng?

Cho dãy số $\left(u_n\right)$ biết $\left\{\begin{array}{l}{u}_1=2\\ u_{n+1}=2u_n \forall n\in \mathrm{\mathbb{N}}*\end{array}\right.$. Tìm số hạng tổng quát của dãy số này ?

Cho hình hộp chữ nhật ABCD.A' B' C' D' có tổng diện tích của tất cả các mặt là 36, độ dài đường chéo AC' bằng 6. Hỏi thể tích của khối hộp lớn nhất là bao nhiêu?

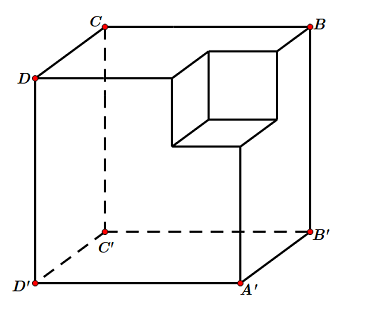
Một khối đa diện (H) được tạo thành bằng cách từ một khối lập phương cạnh bằng 3, ta bỏ đi khối lập phương cạnh bằng 1 ở một “góc” của nó như hình vẽ. Gọi (S) là khối cầu có thể tích lớn nhất chứa trong (H) và tiếp xúc với các mặt (A'B'C'D'),(BCC'B'),(DCC'D'). Tính bán kính của (S).

Cho hình chữ nhật ABCD  có AB = 2a, BC = 3a. Gọi M, N lần lượt là các điểm trên cạnh AD, BC sao cho MA = 2MD, NB = 2NC. Khi quay quanh AB, các đường gấp khúc AMNB, ADCB sinh ra các hình trụ có diện tích toàn phần $S_1,S_2$ Tính tỉ số $\frac{S_1}{S_2}$là:

Đề cương ôn tập chương I môn lịch sử lớp 12 có 30 câu. Trong đề thi chọn ngẫu nhiên 10 câu trong 30 câu đó. Một học sinh chỉ nắm được 25 câu trong đề cương đó. Xác suất để trong đề thi có ít nhất 9 câu hỏi nằm trong 25 câu mà học sinh đã nắm được là. (Kết quả làm tròn đến hàng phần nghìn)

Một hình trụ có bán kính đáy bằng r và khoảng cách giữa hai đáy bằng $r\sqrt{3}$. Một hình nón có đỉnh là tâm mặt đáy này và đáy trùng với mặt đáy kia của hình trụ. Tính tỉ số diện tích xung quanh của hình trụ và hình nón.

Cho hình chóp S.ABCD. Gọi A', B' , C', D' theo thứ tự là trung điểm của SA, SB, SC, SD. Tính tỉ số thể tích của hai khối chóp S.A'B'C'D' và S.ABCD.

Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y = sinx + cosx + mx đồng biến trên $\mathrm{ℝ}$