Trong không gian với hệ tọa độ Oxyz, cho các điểm A(1;0;0), B(0;2;0), C(0;0;3), D(2;-2;0). Có tất cả bao nhiêu mặt phẳng phân biệt đi qua 3 trong 5 điểm O, A, B, C, D
A. 7
B. 5
C. 6
D. 10
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án B
 Ta có thẳng hàng
Ta có thẳng hàng
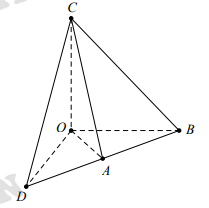
Do đó, 5 điểm O, A, B, C, D tạo thành tứ diện như hình vẽ bên
Vậy có tất cả 5 mặt phẳng cần tìm đó là:
+ Mặt phẳng (OAC) đi qua 3 điểm O, A, C.
+ Bốn mặt phẳng là các mặt bên của tứ diện O.BCD đi qua 3 điểm trong 5 điểm O, A, B, C, D.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Tập nghiệm của bất phương trình có dạng S = [a;b]. Giá trị b - 2a thuộc khoảng nào sau đây?
Cho hàm số y = f(x) liên tục trên và có đồ thị như hình dưới. Biết rằng trục hoành là tiệm cận ngang của đồ thị. Tìm tất cả các giá trị thực của tham số m để phương trình có hai nghiệm phân biệt dương.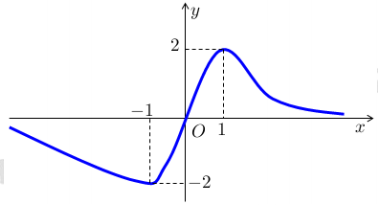
Cho ab, là các số thực dương thỏa mãn . Hỏi giá trị nhỏ nhất của biểu thức sau là:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a. Hai mặt phẳng (SAB) và (SAD) cùng vuông góc với đáy, góc giữa hai mặt phẳng (SBC) và (ABCD) bằng . Tính tỉ số biết V là thể tích của khối chóp S.ABCD?
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P):2x - y + z - 10 = 0 điểm A(1;3;2) và đường thẳng . Tìm phương trình đường thẳng D cắt (P) và d lần lượt tại hai điểm M và N sao cho A là trung điểm của cạnh MN
Tam giác mà ba đỉnh của nó là ba trung điểm ba cạnh của tam giác ABC được gọi là tam giác trung bình của tam giác ABC. Ta xây dựng dãy các tam giác sao cho là một tam giác đều cạnh bằng 3 và với mỗi số nguyên dương , tam giác là tam giác trung bình của tam giác . Với mỗi số nguyên dương n, kí hiệu n S tương ứng là diện tích hình tròn ngoại tiếp tam giác . Tính tổng
Xét tứ diện OABC có OA, OB, OC đôi một vuông góc nhau. Gọi lần lượt là góc giữa các đường thẳng OA, OB, OC với mặt phẳng (ABC). Khi đó giá trị nhỏ nhất của biểu thức 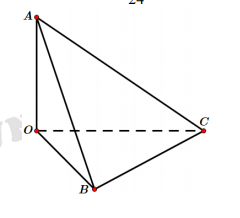
Trong không gian với hệ trục tọa độ Oxyz, cho hai mặt phẳng (P):3x - 2y + 2z - 5 = 0 và (Q):4x + 5y - z + 1 = 0. Các điểm A, B phân biệt thuộc giao tuyến của hai mặt phẳng (P) và (Q). Véctơ cùng phương với vecto nào sau đây?
Cho n là số nguyên dương thỏa mãn . Hệ số của số hạng chứa của khai triển biểu thức bằng:
Biết rằng đồ thị hàm số cắt trục hoành Ox tại 4 điểm phân biệt. Khi đó đồ thị hàm số cắt trục hoành Ox tại bao nhiêu điểm?
Cho hình lập phương ABCD. A’B’C’D’ có cạnh a. Một khối nón có đỉnh là tâm của hình vuông ABCD và đáy là hình tròn nội tiếp hình vuông A’B’C’D’. Kết quả tính diện tích toàn phần của hình nón đó có dạng bằng với b, c là hai số nguyên dương và b > 1. Tính giá trị của bc?
Trong không gian với hệ tọa độ Oxyz, tính khoảng cách từ điểm M(1;2;-3) đến mặt phẳng (P):x + 2y - 2z - 2 = 0
Một hộp đựng 9 viên bi trong đó có 4 viên bi đỏ và 5 viên bi xanh. Lấy ngẫu nhiên từ hộp 3 viên bi. Tìm xác suất để 3 viên bi lấy ra có ít nhất 2 viên bi màu xanh.
Cho hàm số y = f(x) có và . Khẳng định nào sau đây là khẳng định đúng?