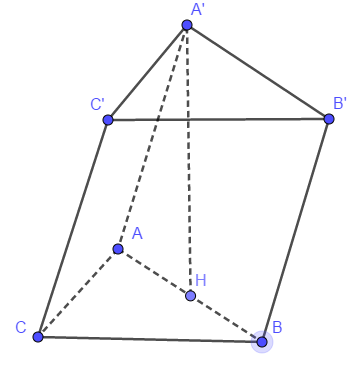
Cho khối lăng trụ \[ABC.A'B'C'\] đáy là tam giác vuông cân tại \[A\]. Hình chiếu của \[A'\] lên mặt phẳng \[(ABC)\] là trung điểm \[H\] của đoạn \[AB\], khoảng cách giữa \[A'H\] và \[BC'\] bằng \[\frac{{4\sqrt 5 }}{5}\] và \[AA' = 3\]. Thể tích khối lăng trụ \[ABC.A'B'C'\] bằng
A.\[\frac{{8\sqrt 5 }}{3}\].
B. \[8\sqrt 5 \].
C. \[16\sqrt 5 \].
D. \[\frac{{16\sqrt 5 }}{3}\].
 Giải bởi Vietjack
Giải bởi Vietjack
Lời giải
Gọi K là trung điểm \[A'B'\] ta có:
+) \[B'KHB\] là hình bình hành nên \[HB'\] cắt \[BK\] tại trung điểm \[I\] của mỗi đường.
\[\begin{array}{l} + )\,BK\parallel A'H \Leftarrow A'H\parallel (BKC') \Rightarrow d(A'H,BC') = d(A'H,(BKC')) = d(H,(BKC'))\\ = d(B',(BKC')) = d = \frac{{4\sqrt 5 }}{5}.\end{array}\]
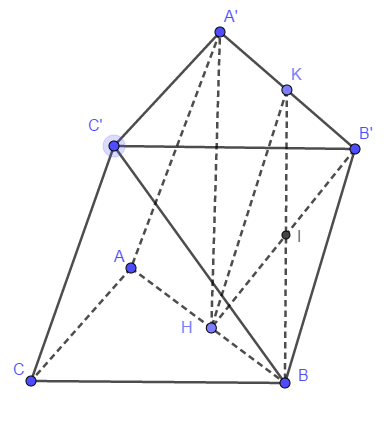
Đặt \[AB = 2x \Rightarrow A'C' = 2x\,.\] (Do đáy là tam giác vuông cân tại \[A\]).
Ta có
\[\begin{array}{l}KC' = \sqrt {A'C{'^2} + A'{K^2}} = x\sqrt {5.} \\KB = A'H = \sqrt {AA{'^2} - A{H^2}} = \sqrt {9 - {x^2}} .\end{array}\]
Xét tứ diện \[B'BC'K\] với đáy là \[\Delta BC'K\] vuông tại \[K\] có \[{S_{BC'K}} = \frac{1}{2}.KC'.BK. = \frac{1}{2}.x\sqrt 5 .\sqrt {9 - {x^2}} .\] và độ dài đường cao là \[d\].\[ \Rightarrow {V_{B'.BCK}} = \frac{1}{3}d.{S_{BKC'}} = \frac{1}{3}.\frac{{4\sqrt 5 }}{5}.\frac{1}{2}x\sqrt 5 .\sqrt {9 - {x^2}} \,\, = \frac{2}{3}\,x.\sqrt {9 - {x^2}} .\,\] (1)
Mặt khác, \[{V_{B'.BCK}} = \frac{1}{6}{V_{ABC.A'B'C'}} = \frac{1}{6}.A'H.{S_{ABC}} = \frac{1}{6}.\sqrt {9 - {x^2}} \,.\frac{1}{2}2x.2x = \frac{1}{3}\,{x^2}.\sqrt {9 - {x^2}} .\,\,(2)\]
Từ (1) và (2) suy ra \[\frac{2}{3}\,x.\sqrt {9 - {x^2}} = \frac{1}{3}\,{x^2}.\sqrt {9 - {x^2}} \Leftrightarrow x = 2.\] \[A'H = \sqrt 5 .\]
Vậy thể tích khối lăng trụ
\[{V_{ABC.A'B'C'}} = A'H.{S_{ABC}} = \sqrt 5 .\frac{1}{2}.{(2x)^2} = \sqrt 5 .\frac{1}{2}.{(2.2)^2} = 8\sqrt 5 .\]
Chọn đáp án B
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Có bao nhiêu cặp số nguyên \(a,\,\,b\) thỏa mãn đồng thời các điều kiện \({a^2} + {b^2} >1\) và \({a^2} + {b^2} - 3 \le {\log _{{a^2} + {b^2}}}\left( {\frac{{{b^2}\left( {{a^2} + {b^2} + 4} \right) + 4{a^2}}}{{{a^2} + 2{b^2}}}} \right)\)?
Cho hàm số \(f(x)\) liên tục trên \(\mathbb{R}\) thỏa mãn \(f(x) = \left\{ \begin{array}{l} - 3{x^2} + 6x + m{\rm{ khi }}x < 1\\\frac{{2x + 1}}{{x + 2}}{\rm{ khi }}x \ge 1\end{array} \right.\) (Với\(m\) là hằng số). Biết \(I = \int\limits_{\frac{1}{e}}^{{e^2}} {\frac{{f\left( {\ln x} \right)}}{x}{\rm{d}}x} + \int\limits_0^{\ln 2} {{e^x}f\left( {{e^x}} \right){\rm{d}}x} = a + b\ln 4 + c\ln 3\) với \(a,\,\,b,\,c\) là các số nguyên. Tổng \(a + 2b + 3c\) bằng
Có tất cả bao nhiêu giá trị nguyên của tham số \(m\) sao cho phương trình \(\log _2^2x - \left( {m + 1} \right){\log _2}x + 2m - 3 = 0\,\)có đúng 2 nghiệm phân biệt thuộc khoảng \(\left( {2\,;\,16} \right)\) ?
Cho hình hộp chữ nhật \[ABCD.A'B'C'D'\]. Gọi \(N\) là trung điểm của \(B'C'\), \(P\) đối xứng với \(B\) qua \(B'\). Khi đó mặt phẳng \(\left( {PAC} \right)\) chia khối hộp thành hai phần. Tính tỉ số thể tích phần lớn và phần bé.
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thoi cạnh \(a\) và \[AC = a.\] Biết tam giác \(SAB\) cân tại \(S\) và nằm trong mặt phẳng vuông góc với mặt phẳng đáy; góc giữa đường thẳng \(SD\) và mặt đáy bằng \(60^\circ .\) Khoảng cách giữa hai đường thẳng \(AD\) và \(SC\) bằng
\(\frac{{a\sqrt {609} }}{{19}}\).
Cho hàm số \(y = \left| {\frac{1}{{x + 3}} - \frac{1}{x} + \frac{1}{{x - 2}} - \frac{1}{{x - 5}} - m} \right|\), với \(m\) là tham số. Có bao nhiêu giá trị nguyên của \(m\) để hàm số đã cho có giá trị nhỏ nhất trên \(\left( { - 3\,;5} \right)\backslash \left\{ {0\,;2} \right\}\) là một số dương?
Thể tích của khối lăng trụ có đáy là hình vuông cạnh 2 và chiều cao 3 bằng
Cho số phức \(z = 2 + mi\,\,\left( {m \in \mathbb{R}} \right)\)thỏa \(\left( {2z - i} \right)\left( {2\overline z - 2} \right)\) là số thực. Giá trị \(\left| {2z - 3} \right|\) bằng
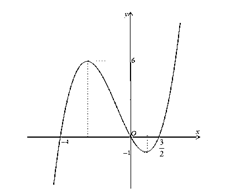
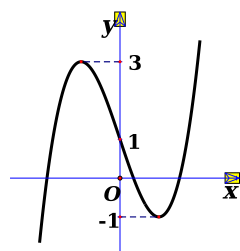
Cho hàm số bậc ba \(y = f(x)\) có đồ thị như hình vẽ bên. Có tất cả bao nhiêu giá trị nguyên dương của tham số \(m\) để phương trình \(\left| {f\left( {{x^3} - 3{x^2}} \right)} \right| - {\log _2}m = 0\) có 8 nghiệm phân biệt?
Trong không gian \[Oxyz\], cho mặt cầu \(\left( S \right):{x^2} + {y^2} + {z^2} - 6x + 4y - 12z + 41 = 0\). Từ điểm \(M\left( {2;\, - 1;\,3} \right)\) kẻ ba tiếp tuyến phân biệt \(MA,\,MB,\,MC\) đến mặt cầu (\(A,\,B,\,C\) là các tiếp điểm). Khi đó phương trình mặt phẳng \[\left( {ABC} \right)\] có dạng \[x + by + cz + d = 0\]. Giá trị \[b + c + d\] bằng
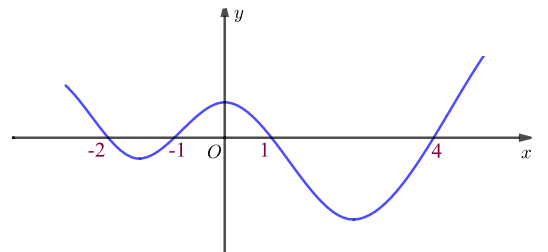
Cho \[f\left( x \right)\] là hàm số đa thức có một phần đồ thị của hàm \[f'\left( x \right)\] như hình vẽ bên. Gọi \[F\left( x \right)\] là một nguyên hàm của hàm số \[f\left( x \right)\]. Tìm tất cả các giá trị của tham số \[m\] để hàm số \[y = F\left( x \right) + \left( {m - 1} \right)x + 2020\] đồng biến trên khoảng \[\left( { - 1\,;\,4} \right)\].
Gọi \(M,\;m\) lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = {x^3} - 3{x^2} + a\) trên đoạn \[{\rm{[ - 1;}}\;{\rm{3]}}\]. Nếu \(M = 2m\) thì khẳng định nào sau đây là đúng?
Cho hàm số đa thức bậc ba \(y = f\left( x \right)\) có đồ thị như hình vẽ bên. Số nghiệm của phương trình \(f\left( x \right)\, = \,0\) là
Bạn muốn mua một áo sơ mi cỡ 40 hoặc 41. Áo cỡ 40 có 6 màu khác nhau, áo cỡ 41 có 4 màu khác nhau. Hỏi bạn có bao nhiêu cách chọn?