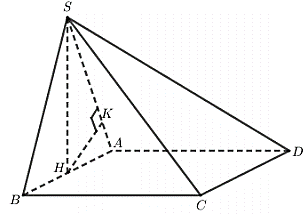
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy. Tính khoảng cách từ điểm C đến mặt phẳng .
A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack
Chọn B
Phương pháp:
Sử dụng lý thuyết về đường thẳng song song với mặt phẳng: Cho hai điểm và mặt phẳng . Khi đó
Cách giải:
Gọi H là trung điểm của AB suy ra
Ta thấy:
(vì H là trung điểm của AB)
Gọi K là hình chiếu của H lên
Lại có
Từ hai điều trên suy ra
Tam giác SAB đều cạnh a nên
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Trong không gian với hệ tọa độ cho điểm . Tọa độ điểm đối xứng với điểm A qua trục Oy là:
Trong không gian Oxyz cho điểm và . Phương trình mặt cầu tâm I và đi qua A có phương trình là:
Trong không gian , cho điểm . Bán kính mặt cầu có tâm và tiếp xúc với mặt phẳng là
Cho tập hợp gồm 17 số nguyên dương đầu tiên. Chọn ngẫu nhiên một tập con có 3 phần tử của tập hợp S. Tính xác suất để tập hợp được chọn có tổng các phần tử chia hết cho 3.
Đường thẳng là giao của hai mặt phẳng và thì có vecto chỉ phương là:
Biết rằng hàm số chỉ nghịch biến trên một đoạn có độ dài bằng 3. Giá trị tham số m thuộc khoảng nào sau đây?
Trong không gian Oxyz, phương trình tham số của đường thẳng đi qua điểm và có vecto chỉ phương là
Trong không gian Oxyz, cho điểm và đường thẳng Mặt phẳng đi qua M và vuông góc với có phương trình là
Trong không gian Oxyz, cho mặt cầu . Tìm số thực m để mặt phẳng cắt theo một đường tròn có bán kính bằng 3.
Hàm số và có đồ thị như hình vẽ dưới đây.
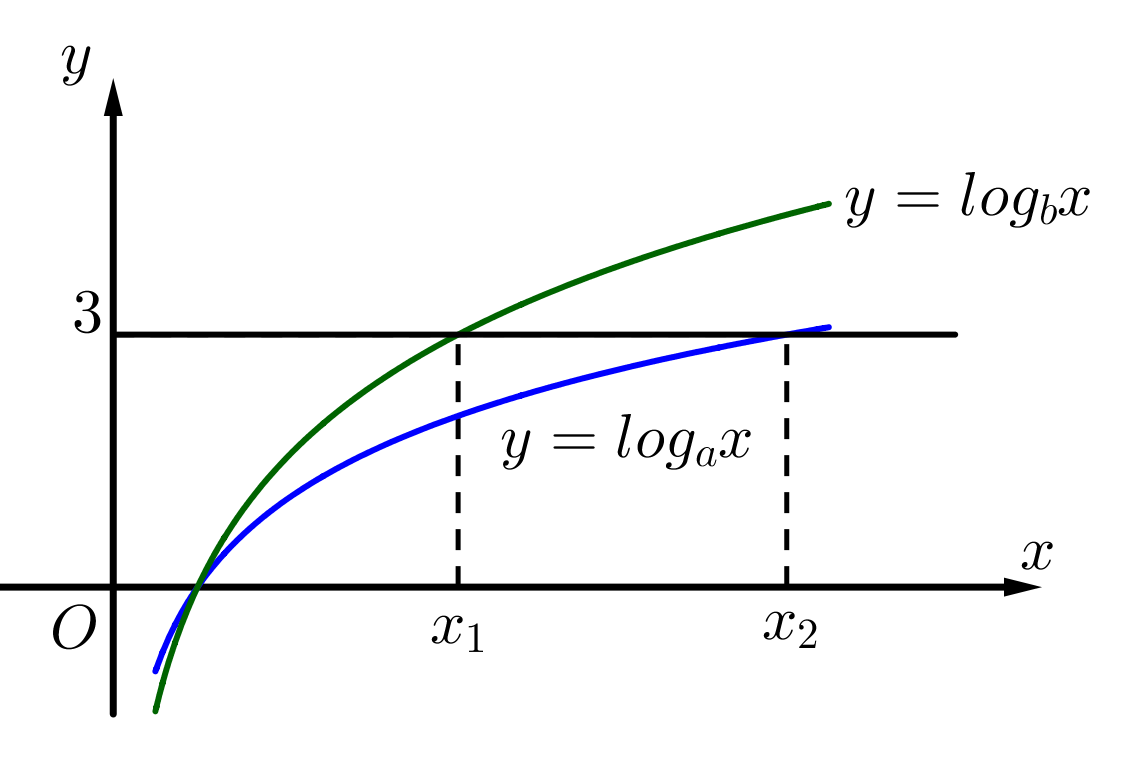
Đường thẳng cắt hai đồ thị tại các điểm có hoành độ , . Biết rằng , giá trị của bằng
Cho bất phương trình . Tìm tất cả các giá trị của tham số để bất phương trình có nghiệm đúng